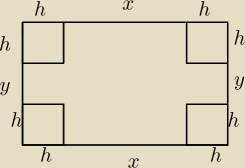
NIrówność średnich Pytający: Cześć, mam pytanie odnośnie zadania z optymalizacją. Dany jest prostokątny arkusz kartonu o długości 80 cm i szerokości 50 cm. W czterech rogach tego arkusza wycięto kwadratowe naroża (zobacz rysunek). Następnie zgięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długość boku wyciętych kwadratowych naroży, dla której objętość otrzymanego pudełka jest największa. Oblicz tę objętość. Chciałbym to rozwiązać za pomocą nierówności o średnich. x+2h=80 y+2h=50 ======= x+y+4h = 130 Am≥Gm

x+y+4h
	≥3√xy*4h
3

130
	≥3√xy*4h
3

przy czym równość zachodzi dla x=y=4h i coś tutaj mi nie pasuje, bo odpowiedź to h=10

ABC: jakoś ty dziwnie to zadanie robisz piszesz "równość zachodzi dla x=y=4h" ale jeśli x=y to x+2h=y+2h , 80=50 i sprzeczność!

Pytający: Więc jak się za nie zabrać?

ABC: to jest klasyczne zadanie na pochodne jeszcze z komunistycznego liceum pamiętam je

Pytający: Ale właśnie chodzi o to aby użyć nierówności między średnimi

wredulus_pospolitus: x*y*h ma być maksymalne więc: (80−2h)*(50−2h)*h ma być maksymalne pochodna i szukasz maksimum (które będzie dla h=10)

Pytający: wredulus_pospolitus to wiem, ale tutaj chodzi o rozwiązanie z wykorzystaniem nierówności między średnimi

wredulus_pospolitus: Pytałeś się jak się za to zabrać, to dostałeś odpowiedź. Zauważ, że równości A_m = G_m NIGDY nie będzie, ponieważ masz zadany warunek: x > y co wynika z treści zadania. Więc wracasz do funkcji wielomianowej stopnia 3.

Pytający: Dziękuję za odpowiedź