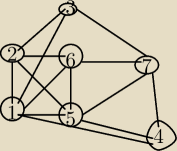
GRAFFFFFFFFFFFFFFFFFFFFFFFFFY Snooopy: Mam za zadanie wypisać wszystkie wierzchołki, podać ich stopnie, wypisać macierze krawędzi oraz wszystkie ścieżki między 1, a 5 o długości maks 4. wierzchołki to 1, 2, 3, 4, 5, 6, 7 stopnie kolejno 5, 4, 3, 3, 7, 4, 4 macierze krawędzie, czyli duża tabelka, którą, wydaje mi się, mam w porządku. Czy na podstawię tego rysunku (starałem się odwzorować w 100%) krawędzie między 1 i 5 oraz 5 i 4 są wielorotne? Czyli ścieżka między 1 i 5 (najkrótsza) jest możliwa na dwie opcje. krawędź (1−5)₁ oraz krawędź (1−5)₂

Snooopy: i wówczas wszystkie ścieżki to: 1−5₁ 1−5₂ 1−2−5 1−6−5 1−2−6−5 1−6−7−5 1−3−7−5 Ps. tak, na samej górze jest 3, a wierzchołki 1 i 4 nie są połączone bezpośrednio

Saizou : Długość ścieżki to liczba krawędzi, więc nie masz wpisanych ścieżek o długości 4

Snooopy: Mhm, a czy mogę wrócić do tego samego wierzchołka? Chodzi mi dokładniej o ścieżkę np. 1−2−3−1−5

Snooopy: Czy idę tylko do przodu i rozwiązaniami ( z 4 krawędziami) będą : 1−2−3−7−5 1−2−6−7−5 1−6−7−4₁−5 1−6−7−4₂−5

iteRacj@: Sprawdź, jak masz zdefiniowaną ścieżkę, będziesz wiedzieć, czy krawędzie i wierzchołki mogą się powtarzać.