ee Mięsarz: Dwie wysokości trójkąta ABC zawierają się w prostych k: 5x−3y+5=0 oraz l: x+y−1=0. Wiedząc ponadto ,że A(−2,1), wyznacz równania ogólne prostych, w których zawierają się boki tego trójkąta.

Mięsarz: Nikt nie wie?

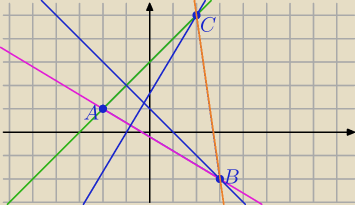
Eta: Moja odp: AB: 3x+5y+1=0 AC: x−y+3=0 BC: 7x+y−19=0 ==============

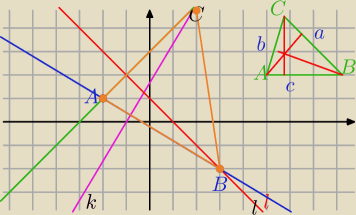
Mila: k: 5x−3y+5=0 oraz l: x+y−1=0.

	5		5
k: y=		x+
	3		3

l: y=−x+1 Wysokości Δ przecinają się w jednym punkcie: 1) Prosta AB ⊥h_c

	3		−3		1
y=−		x+b i 1=		*(−2)+b, b=−
	5		5		5

	3		1
AB: y=−		x−		⇔
	5		5

AB: 3x+5y+1=0 wsp. punktu B

	3		1
−		x−		=−x+1
	5		5

B=(3,−2) 2) AC⊥h_b AC: y=x+b i 1=−2+b, b=3 AC: y=x+3⇔ AC: x−y+3=0 wsp. Punktu C

	5		5
x+3=		x+
	3		3

x=2, y=5 C=(2,5) 3) Pozostaje Ci równanie prostej BC

Mięsarz: Dziękuję właśnie zrobiłem Pozdrawiam i dobranoc

Eta: 2 sposób z warunku prostopadłość z wykorzystaniem wektorów AB ⊥ k wektor k [5,−3] wektor AB [3,5] AB: 3(x−x_A)+5(y−y_A)=0 ⇒ AB: 3(x+2)+5(y−5)=0 AB: 3x+5y+1=0 itd............

Mila: