geometria analityczna vvool: Punkt A(−2,5( jest wierzchołkiem Δ równobocznego ABC, a punkt S(4,11) jest środkiem okręgu wpisanego w ten Δ oblicz współrzędne wierzchołków B i C.

the foxi: AS=2SD, gdzie D jest środkiem boku naprzeciw wierzchołka A 2[6;6]=2[x_D−4;y_D−11] [6;6]=[2x_D−8;2y_D−22] 2x_D−8=6 ⇒ x_D=7 2y_D−22=6 ⇒ y_D=14 D=(7;14) AD=[9;9] ⇒a_AD=1 ⇒ a_CB=−1 równanie prostej przechodzącej przez punkt D: y=−(x−7)+14=−x+21 dalej dokończysz?

vvool: spróbuję ale na pewno mi to chwile zajmie

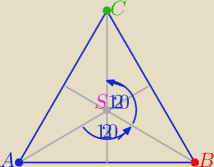
Eta: A ja tak z obrotu punktu A wokół punktu S o kąt 120^o otrzymam B a z obrotu punktu A o kąt 240^o otrzymam C Równania obrotu: ( kiedyś uczono w szkole średniej B(x^',y^') x^'=(x_A−x_S)*cosα− (y_A−y_S)*sinα+x_S y^'=(y_A−y_S)*cosα+(x_A−x_S)*sinα+y_S i mamy odp........... wiedząc,że sin120^o= ... cos120^o =.... sin240^o=.... cos240^o=....

vvool: A(−2,5) D(7,14) 5=−2a+b 14=7a+b 9=9a a=1 5=−2+b b=7 y_AD=x+7 y_CB=−x+b, D(7,14) 14=−7+b b=21 y_CB=−x+21 AD=[9;9] haha no nie mam pomyslu na the foxi sposob zastanawialem sie ale brakuje mi wiedzy widocznie jeszcze! ale trzeba to zmienic niby cos kombinuje ale nieskutecznie i raczej sam nie wymysle dalej nic ale ogarnalem ten twoj sposob z wektorow tylko co dalej dajcie wskazowki to pokminie dalej bo brakuje mi punktu zaczepnego

vvool: jeszcze jedno mi sie nasunelo do glowy jesli wyznaczyc prosta AC gdzie A(−2,5) C(x_c,y_c) i potem dlugosc odleglosci prostej od punktu dlugosc znam bo to jest rowne SD i bede mial 2 punkty czy ma to sens?

Satan: Eta, teraz to studia na pierwszym roku, na algebrze liniowej