funkcja kwaadratowa geometria : Funkcja kwadratowa f jest określona wzorem f(x)=−¹₄x²+x+2. Różnica między największa i najmniejszą wartością funkcji f w przedziale <0;k>, gdzie k>3 wynosi 5. Oblicz k.

wredulus_pospolitus: x_wierzchołka = 2 −> f(2) = 3 dla k>4 to f(k) < f(0) = 2 więc mamy: 3 − f(k) = 5 −> f(k) = −2 −> k =

geometria : dokładnie tak samo probowałem zrobic ale nie wiedzialem co dalej ¹₄k²−k−4=0 k=2+2√5 v k=2−2√5 i tu utknąłem

Satan: No i jak to co dalej? (Tu zakładam, że dobrze masz policzone wartości k) Szacowanie. k > 3, tak? No to sprawdzamy: 2 + 2√5 (?) > 3 2√5 > 1

	1
√5 >
	2

A to już oczywiste, że prawda. W drugim przypadku wyjdzie −2√5 > 1, co jest oczywiście fałszem, bo jak liczba ujemna może być większa od dodatniej? Wniosek...?

Mila:

	1
f(x)=−		x2+x+2.
	4

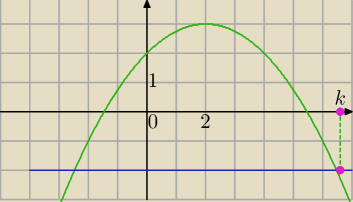
x_w=2 y_w=3 f(0)=2 1) Największa 3, najmniejsza 2 w przedziale <0,2> 3−2=1 2) dla x≥2 największa f_max(2)=3 i funkcja jest malejąca. 3−y=5 różnica wartości y=−2

	1
−		x2+x+2=−2
	4

1
	x2−x−4=0 i x>2
4

	1
Δ=1+4*4*		=1+4=5
	4

	1−√5		1+√5
x1=		<0 lub x2=		=2+2√5
	12		12

	1
f(2+2√5)=−		(2+2√52+(2+2√5)+2=−(1+2√5+5)+2+2√5+2=
	4

=−6−2√5+4+2√5=−2 3−(−2)=5 różnica między najmniejszą i największa wartością w przedziale <0,2+2√5>