okrAG geometria : Okrąg o środku S przecina oś OX w punktach O(0,0) i A. Odcinek OM, gdzie M(6,2pierwiastki z 3) jest średnicą tego okręgu. Oblicz pole wycinka kołowego wyznaczonego przez krótszy łuk MA okręgu

wredulus_pospolitus: 1) OM jest średnią −−− połową tego odcinka to środek okręgu 2) Mając środek okręgu i jego promień (czyli połowa średnicy czyli połowa długości odcinak OM) masz wzór na tenże okrąg 3) Do powyższego wzoru podstawiasz y=0 i sprawdzasz jaki 'x' wyjdzie ... masz współrzędne punkt A Dalej chyba sobie poradzisz, prawda ?!

geometria : Wyszło mi średnica 4√3 Wzór (x−3)²+(y−√3)²=12 r=2√3 Pole wycinka 2π Bo kąt 60^o mozesz spr czy dobrze

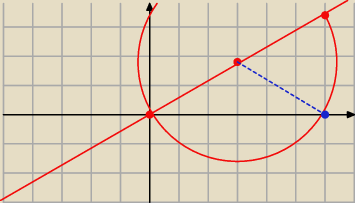
wredulus_pospolitus: średnia − dobrze promień − dobrze środek okręgu − dobrze ale kąt mi się nie podoba, już z rysunku widać, że ten kąt powinien być kątem rozwartym

wredulus_pospolitus: ewentualnie inny sposób rozwiązania: 1) zauważamy, że Δ_OAS jest równoramienny

	√3
2) wyznaczamy kąt nachylenia prostej zawierającej OM (tgα =		−> α = 30o)
	3

3) w takim razie ∡OSA = 180 − 2*30 = 120^o

wredulus_pospolitus: aaaaa ... to MA miało być ... no to dobrze wyznaczone

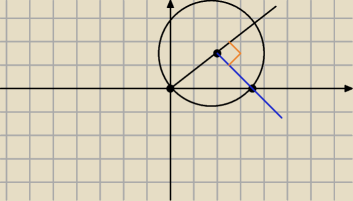
geometria : Czemu dobrze na rysunku widać, że jest 60 stopni