wielomiany sylwiaczek: rownanie 2x³ − x² − 2x + 6 = 0 ma pierwiastek wymierny nalezacy do przedzialu: a. (−6, −2> b. (−2, 0> c. (0, 2> d. (2, 6> wiem, ze trzeba p/q ale wtedy mi wychodzi +/− 1/2, 1, 3/2, 2, 3, 6 i nie wiem co dalej xd

Kingaa: Wtedy z ^p_q musisz po kolei wstawiać i szukać pierwiastka, ale w tym wypadku nie będzie to pierwiastek wymierny więc żadna z propozycji nie wyzeruje wielomianu. Ja bym to zrobiła powołując się na tw, Darboux. Po kolei wstawiasz końce podanych przedziałów i patrzysz jaką masz wartość w(x), czy jest dodatnia czy ujemna. a. w(−6)= −450 w(−2)=−10 => że w tym przedziale wykres wielomianu nie przecina osi OX, więc nie ma miejsc zerowych. b. w(−2)=−10 w(0)=6 => że w wybranym przedziale wykres przecina oś OX, czyli jest to nasz szukany przedział

wredulus_pospolitus: w(x) = 2x³ − x² − 2x + 6 w(0) = 6 w(2) = 16 − 4 − 4 + 6 > 0 więc (raczej) nie ma pierwiastka w przedziale (0,2) w(−2) = −16 − 4 + 4 + 6 < 0 więc na pewno jest jakiś pierwiastek w przedziale (−2,0) z wymiernych pierwiastków w tym przedziale mamy: −1/2 , −1, −3/2 podstawiamy te trzy i sprawdzamy czy któryś z nich jest pierwiastkiem Powyższa metoda jest metodą radzenia sobie 'na teście'. Inną metodą jest po prostu podstawienie każdej z tych 12 wartości.

wredulus_pospolitus: Kinga −−− to że funkcja wielomianowa stopnia 3 ma f(q) < 0 i f(p) < 0 nie jest jednoznaczne z tym, że ów funkcja nie przecina osi OX w przedziale (q,p)

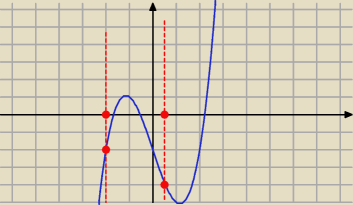
wredulus_pospolitus: oto przykładowa funkcja ( f(x) = x³ − 4x − 2 )

Kingaa: wredulus pospolitus masz rację, ale funkcja 3 stopnia przecina oś OX co najmniej raz i szukamy takiego przedziału, w którym ona będzie się zerowała. Dlatego często przedział (q,p) może być za duży więc szukamy innego, gdzie wartości na końcach będą różnego znaku.

Kingaa: Funkcja przecina, ale nie można tego w jakiś ładny sposób opisać, dlaczego tak właśnie się dzieje

wredulus_pospolitus: Kingaa ... więc o co Ci chodziło i wiem dlaczego tak robiłaś ... zwłaszcza że ja zrobiłem identycznie, tylko −−− zauważ, że ja napisałem "raczej", a Ty napisałaś "nie przecina". Zwróciłem uwagę tylko po to by ktoś z czytających nie miał błędnego przeświadczenia i nie zrobił błędu w podobnym zadaniu, ale przy innej funkcji.

wredulus_pospolitus: Kingaa −−− i druga sprawa ... sprawdzenie w(p) < 0 i w(q) > 0 także nie jest końcem zadania ... bo pierwiastek musi być wymierny (a w przedziale (−2,0) mogło się okazać, że pierwiastek będzie niewymierny)

Kingaa: Masz rację, nie doczytałam

ABC:

	3
−		jest pierwiastkiem wymiernym i rozkład 2(x+32)(x2−2x+2)
	2

pozostałe pierwiastki nie są rzeczywiste: 1−i,1+i