Pokaż, że − ln(1 − x) ≥ sin x dla x ∈ [0, 1[ Natalia: Pokaż, że − ln(1 − x) ≥ sin x dla x ∈ [0, 1[

M:

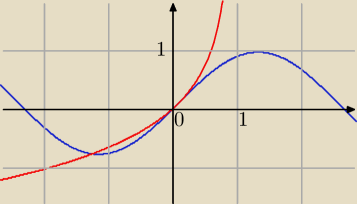
abcd: Należy wykazać, że Δ = − ln(1 − x) − sin x ≥ 0 dla x ∈ [0, 1[. Rozwijam funkcje −ln x i sin x w szereg potęgowy: −ln(1− x) = x + x²/2 + x³/3 + x⁴/4 +...+ x^k/k +... sin = x − x³/6 + x⁵/125 − x⁷/7! + ... (−1)^k x^2k+1/(2k+1)! +... Stąd Δ = x²/2 +(x³/3 + x³/6) + x⁴/4 + (x⁵/5−x⁵/125) + ... Z powyższego widać, że wszystkie składniki szerego Δ są dodatnie. cbdo