rekurencja Surykatek: Pytanie dotyczące wskazówki do zadania: równanie rekurencyjne a_n+2=a_n+1*a²_n Wskazówka: rozważ ciąg x_n=log₂a_n Czy podstawa proponowanego logarytmu wynika z podnoszenia wyrazu ciągu do drugiej potęgi?

jc: Nie ma znaczenia, choć może mieć związek z warunkami początkowymi. Czy były podane?

Surykatek: a₀=1 a₁=2

Surykatek: Pytanie odnośnie ostatecznego zapisu: (³√2)²ⁿ ____________ (³√2)⁽⁻¹⁾ⁿ rozumiem rozwiązanie do przedstawionego momentu, dlaczego jednak powyższe wyrażenie wynosi ³√2? Czy przedstawilibyście wykonane operacje na potęgach?

jc: x₀=0, x₁=1, w przypadku logarytmu o podstawie 2. x_n+2 = x_n+1+2x_n z²=z+2, z=2 lub z=−1 x_n=A2ⁿ + B(−1)ⁿ 0=A+B, 1=2A−B, A=1/3, B=−1/3 x_n=(2ⁿ − (−1)ⁿ)/3 a_n=2^x_n = (2^1/3)^2n−(−1)n 2^1/3=³√2 Dalej wzór: a^k−m=a^k/a^m

Surykatek: Intryguje mnie 2ⁿ−(1)ⁿ Ostateczna odpowiedź w notatkach to ³√2. (Rozumiem wszystko, co napisałeś i do danego momentu rozwiązałem). Czy w notatkach występuje błąd, czyli wynik wynosi: (³√2)²ⁿ 2ⁿ−(1)ⁿ= 2ⁿ − ¹₂n + ¹₂n = 2ⁿ

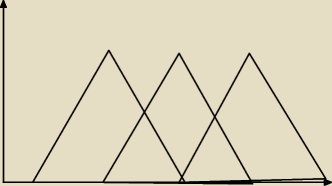
ciosięciosięstało: Porównaj wykresy funkcji przynależności dla funkcji logicznej: F=(x ∊ A) I (x ∊ B) LUB (x ∊ C) różnych realizacji norm T i S obrazek przedstawia to co wyglada obrazek do zadania wykres 1 – iloczyn Hamachera i suma Hamachera, wykres 2 – suma ograniczona i iloczyn ograniczona różnica

Surykatek: Mój drogi, o czym do mnie piszesz?...