Równanie z wartością bezwzględną
vedkav: Proszę o pomoc
Rozwiąż równanie
|x2−2x|≥x3
18 sty 21:49
Eta:
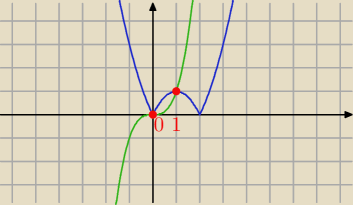
18 sty 21:52
vedkav: A jak się za to zabrać algebraicznie?
18 sty 22:11
Eta:
Przedziałami .....
1/ x∊(−∞, 0> U <2,∞)
.........................
2/ x∊(0,2)
...........................
działaj .....
18 sty 22:21
Mila:
Algebraicznie:
|x2−2x|≥0 dla każdego x∊R
x3<0 dla x<0 wtedy nierówność jest spełniona dla każdego x<0
lub
Dla x∊<0,2>
|x2−2x|=−x2+2x
−x2+2x≥x3⇔
x3+x2−2x≤0
x*(x2+x−2)≤0⇔
x=0,x=−1,x=1
x≤−1 lub x∊<0,1> i x∊<0,2>⇔
x∊<0,1>
lub x>2
|x2−2x|=x2−2x|
x2−2x≥x3
x3−x2+2x≤0
x*(x2−x+2)≤0
x>0, Δ=−7 wyrażenie z lewej dodatnie⇔brak rozwiązań w tym przedziale
odp.
x∊(−∞,1>
18 sty 22:21
Eta:
niebieski wykres nad
zielonym wraz z punktami wspólnymi
odp: x∊(−
∞, 1>
============
I widać jaką przewagę ma rozwiązanie graficzne nad rozwiązaniem algebraicznym !

18 sty 22:31
ICSP: |x2−2x|≥x3
Dla x > 0
(x3 − x2 + 2x)(x3 + x2 − 2x) ≤ 0
x2[x2 − x + 2][x2 + x − 2] ≤ 0
x2 + x − 2 ≤ 0
(x+2)(x−1) ≤ 0
x ≤ 1
Ostatecznie
x ∊ (−∞ ; 1]
18 sty 22:44
Eta:
Graficznie jeszcze szybciej !

18 sty 22:47
ICSP: Zakładając, że rozwiązujący potrafi narysować wykres.
18 sty 22:53
Mila:
To akurat prosty wykres

18 sty 22:55
Maciess: No nie wiem czy x
3 to tak ładnie bym narysował od razu

18 sty 23:01
Mila:
Wykres f(x)=x
3 trzeba znać, to często się przydaje.

18 sty 23:39





