parametr dzień dobry: Witam, mam problem z zadaniem: Dla jakich wartości parametru a równanie |x+a| = 1− ||x−2| −3| ma dokładnie 2 rozwiązania? Po narysowaniu wykresu mam cztery rozwiązania a=2 v a=0 v a= −4 v a= −6, jednak w odpowiedzi podane są przedziały. Ktoś mógłby pomóc?

ite: Też rozwiązałam graficznie, ale moje rozwiązanie to wartości parametru z (−6,−4)U(0,2). W jaki sposób rozwiązujesz?

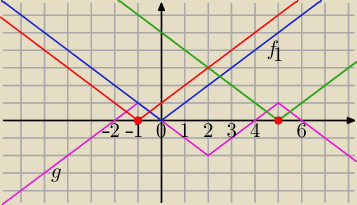
Mila: |x+a| = 1− ||x−2| −3| f(x)=|x+a|=|x−(−a)| f₁(x)=|x| Wykres f(x) powstaje przez przesunięcie wykresu f₁(x) o wektor v=[−a,0] g(x)=1−||x−2|−3| 1) Przesuwamy wykres f₁(x) tak , aby "szpic" znalazł się w przedziale (−2, 0) lub (4,6) −2<−a<0 /*(−1) 2>a>0 lub 4<−a<6 /*(−1) −4>a>−6 odp. a∊(0,2)∪(−6,−4) ====================

Eta: 2 sposób algebraicznie równanie |x−(−a)| ma dwa rozwiązania gdy prawa strona jest>0 czyli gdy ||x−2|−3|<1 to |x−2|−3<1 i |x−2|−3>−1 |x−2|<4 i |x−2|>2 x ∊(−2,6) i x∊(−∞,0)U(4,∞) część wspólna x∊(−2,0) U (4,6) zatem −a∊[(−2,0)U(4,6)] ⇒ a∊[(−6,−4)U (0,2)] =================

Mila: Pięknie