matematykaszkolna.pl
trapezy edek4: Odcinek łączący środki ramion trapezu ma długość 10cm a odcinek łączący środki przekątnych ma długość 3cm. Oblicz długości podstaw trapezu.
16 lut 21:15
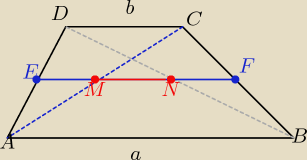
Eta: rysunek z podobieństwa trójkątów: w skali k=2 IEMI= 12b i INEI= 12b
 a−b 
IMFI= 12a => IMNI= IMFI− INFI= 12a − 12b =
 2 
 a−b 
IMNI=
 2 
 1 a−b 1 a−b +2b a+b 
IEFI=
b+
+
b =
=
 2 2 2 2 2 
 a+b 
IEFI =
 2 
zatem: Odcinek łączacy środki ramion −−−− to środkowa trapezu
 a+b 
jej długość to: IEFI=
= 10
 2 
więc a+b= 20 dł.odcinka łaczącego środki przekątnych to: IMNI
 a−b 
długość IMNI =
= 3
 2 
to a −b= 6 mamy układ równań: a+b= 20 a −b= 6 −−−−−−−−− 2a = 26 => a=13 to b= 7
16 lut 23:02
momo: Popełniłeś spory błąd, bo ma wyjść 12 i 8 emotka
15 gru 20:28
Eta: Raczej to ty popełniłeś błąd, ma wyjść 13 cm i 7 cm, wszystko elegancko zrobione, dzięki!
11 kwi 00:23
Marcin: Pamiętaj! Eta zawsze prawidłowo rozwiązuje zadania emotka
11 kwi 00:31
Piotr: ale ostatni post Ety to chyba sie ktos podszyl
11 kwi 00:32
Marcin: Trochę niefajnie, że można się bezproblemowo pod kogoś tutaj podszywać, nie? emotka
11 kwi 00:34
Piotr: to juz bylo. nie ma kolorku − to nie ta osoba, nick zarezerwowany. bedzie 'czarny' Marcin to raczej nie Ty emotka
11 kwi 00:36
Marcin: Właśnie czasem się tutaj taki czarny Marcin pojawia. Irytująca sprawa emotka Nick zarezerwowany? hmm bardziej kolor
11 kwi 00:38
Piotr: no masz − rezerwacja nicka gdy klikniesz Twoj nick. Ja bylem od poczatku logowania wiec nie mialem problemu emotka kolorowego Piotra nie bedzie. no chyba, ze Trivial
11 kwi 00:40
Marcin: Klikniesz mój nick a w wyszukiwarce jest każdy Marcin emotka
11 kwi 00:45
Piotr: wiem emotka ale gdy pojawi sie czarny Marcin i spyta : jak rozwiazac x2 −3x =0 ? To raczej nie Ty emotka
11 kwi 00:49
Marcin: Może coś mi kiedyś odbije i zapomnę jak to rozwiązywać
11 kwi 00:51
Piotr: za zdrowie
11 kwi 00:52
BoosterXS: Mógłby ktoś wyjaśnić z jakiej własności wynika, że jak połączymy środki przekątnych to odcinek ten leży na odcinku łączącym środki ramion? Czy w dowolnym trapezie coś takiego zachodzi?
25 mar 13:08
wredulus_pospolitus: To zachodzi w dowolnym trapezie a wynika z .... tw. Talesa tudzież jak wolisz z podobieństw trójkątów
25 mar 13:10
a7: https://matematykaszkolna.pl/strona/533.html
25 mar 13:12
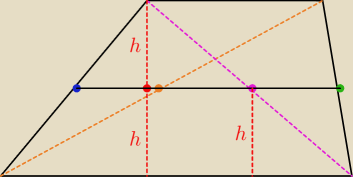
wredulus_pospolitus: rysunek narysowałem 'wysokości' dla pokazania fioletowej przekątnej ... analogicznie się robi dla drugiej oraz dla ramion trapezu
25 mar 13:13