geometria analityczna maciek: dane sa punkty A(−8,1) oraz B(10,11) oraz prosta l: x−y+3=0 a) Wyznacz punkt C leżący na prostej l równoodległy od punktu A i B b) Wykaż, że trójkąt ABC jest prostokątny l: y=x+3 C(x,x+3) z warunku |AC|=|BC| wychodzi mi, że x=24... tak na pewno nie może być nawet na rysunku widać Pomocy

Jack: i jak tam, co sprawia trudnosc w zadaniu ?

maciek: to może tak wyjść?

wredulus_pospolitus: A jak doszedłeś do wyniku x=24

wredulus_pospolitus: Ciekawe jest też to, że ABC ma być trójkątem prostokątnym ... coś tutaj mocno namieszane jest

maciek: ah A(8,1)

Eta: A(8,1) , B(10,11) i C(x,x+3) |AC|²=|BC|² ⇒ .......... x= 4 to y=7 C(4,7) to teraz W Δ ABC : |AC|²=52 i |BC|²= 52 i |AB|²=104 wniosek ...................

jc: C leży na przecięciu prostej y=x+3 i symetralne odcinka AB. A=(8,1) (gubisz =!) B=(10,11)

	1
środek =		(A+B)=(9,6),
	2

wektor prostopadły do symetralnej =B−A= (2,10) || (1,5) symetralna: x+5y=9+30=39 przecięcie, czyli punkt C: x+5(x+3)=39 6x=39−15=24 x=6, y=6+3=9

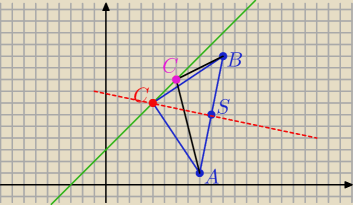
Eta: @ jc Mój C(4,7) leży też na symetralnej A Twój C(6,9) ?

Eta: Aaaaaaaaa widzę chochlika rachunkowego 24/6= 4 a nie 6 jak napisałeś