kombinatoryka mexx: 7. Losowo wybieramy liczbę k ze zbioru {1, 2, 3, 4}, a następnie rzucamy k razy sześcienną kostką. Oblicz prawdopodobieństwa zdarzeń: B iloczyn wyrzuconych oczek będzie liczbą parzystą C : suma wyrzuconych oczek będzie mniejsza niż 22.

wredulus_pospolitus: C) Najłatwiej będzie z przeciwnego ... co musi się stać aby suma wynosiła co najmniej 22? Musisz rzucić 4 kostkami i muszą wypaść: 5,5,6,6 lub 5,6,6,6 lub 6,6,6,6 liczysz jaka jest na to szansa i robisz 1 − to co obliczyłeś

Maciess: Wydaje mi się że najłatwiej będzie policzyć prawdopodobieństwo zdarzenia przeciwnego − czyli iloczyn oczek jest nieparzysty. Dlaczego? Bo tylko wtedy wtedy jest nieparzysty jak występuja same nieparzyste czynniki (mniej mozliwości)

wredulus_pospolitus: B) aby iloczyn był parzysty, przynajmniej jedna z wyrzuconych kostek musi być liczbą parzystą Więc tutaj także z przeciwnego będzie szybciej Dla każdego przypadku (liczby rzucanych kostek) rozpatrujesz tylko sytuacje kiedy wszystkie kostki będą miały nieparzyste cyfry wylosowane 1 − to co policzyłeś i po krzyku.

Maciess: a) Zdarzenie przeciwne liczby postaci (N nieparzysta) N,NN,NNN,NNNN k

	1		3		1
1)		*		=
	4		6		8

	1		3		1
2)		*(		)2=
	4		6		16

	1		3		1
3)		*(		)3=
	4		6		32

	1		3		1
4)		*(		)4=
	4		6		64

	15		49
P(A')=		⇒ P(A)=
	64		64

Maciess: @wredulus_pospolitus skontrolujesz?

mexx: A jak dojść do tego ile będzie tych liczb nieparzystych? W sensie przy losowaniu. Czy to będzie np. ¹₄ dla k=2?

wredulus_pospolitus: Maciess Ci to rozwiązał ... przeanalizuj

	1		1
Tak ... to będzie		(sama kwestia wylosowania NN, ale pamiętać trzeba o
	4		4

odpowiadającej za możliwość rzucania dokładnie dwa razy kostką)

mexx: ok, już to widzę dziękuję bardzo za pomoc

wredulus_pospolitus:

	1		1		15
P(A') =		*(1 − (		)4) =
	4		2		64

Więc jest ok Maciess

maxi: Dla funkcji liniowej g g(15)= −10 i g(−2014)= 2019 Jakie jest miejsce zerowe funkcji g

maxi: Przepraszam ale nie wiem jak założyć nowy post

Eta: Na górze na niebiesko masz napisane dodaj nowe zadanie kliknij i dodaj

Eta: x+y= 15−10=5 i x+y=−2014+2019=5 to x+y=5 ⇒ y= −x+5 x_o = 5 ======

Satan: @Eta, a cóż to za rozwiązanie? Mogłabyś wytłumaczyć? Coś w nim niby widzę, ale nie do końca, a wydaje się być ciekawe

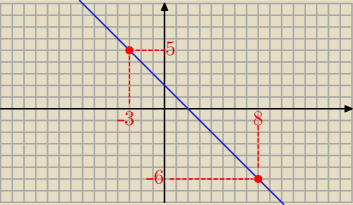
Eta: f(x₁)=y₁ i f(x₂)= y₂) dla funkcji liniowej jeżeli x₁+y₁ = k=x₂+y₂=k to oznacza ,że prosta wyznaczona przez te dwa punkty (x₁,y₁) i x₂,y₂) jest wyznaczona przez wszystkie inne x+y=k i jej równanie jest : y= −x+k Np: f(−3)= 5 i f(8)= −6 to x+y= 2 ⇒ y=−x+2 −−− równanie tej prostej

Satan: Fajnie, już rozumiem. Dziękuję Zakładam, że nie ma uogólnienia na inne współczynniki przy argumencie funkcji niż −1, prawda?