ostrosłup z wpisaną kulą mexx: Krawędź boczna ostrosłupa prawidłowego sześciokątnego jest nachylona do podstawy pod kątem 60 stopni. Oblicz stosunek długości promienia kuli wpisanej w ten ostrosłup do jego wysokości. Bardzo proszę o pomoc.

mexx:

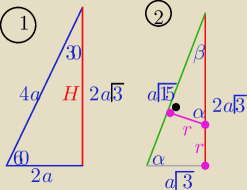
Eta: z 1/ H=2a√3 z 2/ z podobieństwa :

a√15		r		r
	=		⇒		=√5
a√3		2a√3−r		2a√3−r

	a√3(√5−1)
r=
	2

r		√5−1
	=
H		4

================ teraz jest ok

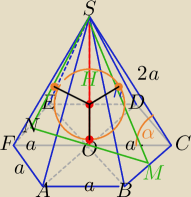
Mila: α=60^o 1) Kula jest styczna do wszystkich ścian ostrosłupa

	2a√3
H=		=a√3
	2

	a√15
h=		z tw. Pitagorasa w ΔBMS
	2

Promień okręgu wpisanego w ΔSMN = promieniowi kuli

	a√3
|MN|=2*		=a√3
	2

	1		3
PΔMNS=		*a*√3*a*√3=		a2
	2		2

	a√3+2h
PΔMNS=		*r
	2

3		(a√3+a√15
	a2=		*r /:a
2		2

3a=(√3+√15)*r

	3a
r=
	√3+√15

===============

r		3a		1		3
	=		*		=
H		√3+√15		a√3		3+√45

r		3
	=
H		3+3√5

r		1
	=
H		1+√5

r		√5−1
	=
H		4

===============

Eta: Sorry odwrotnie wpisałam proporcję ( ale liczyłam dobrze

a√15		2a√3−r
	=		⇒ ..........................
a√3		r

itd

Mila: Promień kuli wpisanej w ostrosłup Liczyłam z wzoru z linka http://www.maturzysta.info/pdf_portal/kula_i_ostroslup.pdf i coś inaczej mi wychodzi. Może Tobie Eto wyjdzie to samo.

Mila: W Twojej metodzie, mniej obliczeń

Eta:

Mila: Ponaglał i co?

Eta: Przepisał ..... i ma w ....

mexx: Dziękuję Wam bardzo za rozwiązanie, bo kompletnie nie miałam pojęcia jak się wziąć za to zadanie