Wyznacz klasy równoważności qw: 1. Wyznaczyć klasy równoważności (klasy abstrakcji) następującej relacji równoważności w zbiorze A = {0,1,2,3,4} R = {(0,0),(0,4),(1,1),(1,3),(2,2),(3,1),(3,3),(4,0),(4,4)}. 2. Wyznaczyć klasy równoważności następujących relacji równoważności R1 = {(x,y) ∈R²: x = y} R2 = {(a,b) ∈A²: a ≡ b (mod 4)}, gdzie A = {1,2,3,...,20} Proszę również o wytłumaczenie w miarę proste jak sie to robi i o co w ogóle chodzi.

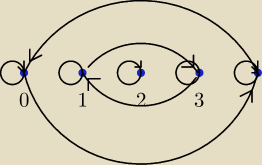
iteRacj@: 1/ relacja ma trzy klasy abstrakcji [0]_R={0,4} [1]_R={1,2} [2]_R={2}

iteRacj@: 2/ R₂ = {(a,b) ∈A²: a ≡ b (mod 4)}, gdzie A = {1,2,3,...,20} [0]_R={4,8,12,16,20} [1]_R={1,5,9,13,17} [2]_R={2,6,10,14,18} [3]_R={3,7,11,15,19}

qw: Na pewno nie tak? [0]r={y∈A: (0,y)∈R}={0,4} [1]r={y∈A: (1,y)∈R}={1,3} [2]r={y∈A: (2,y)∈R}={2} [3]r={y∈A: (3,y)∈R}={1,3} [4]r={y∈A: (4,y)∈R}={0,4} I R1 nie ma klas abstrakcji czy ma 1?

iteRacj@: [0]_R to ta sama klasa abstrakcji co [4]_R [1]_R to ta sama klasa abstrakcji co [3]_R w moim zapisie miało być [1]_R={1,3} tak jak widać na diagramie

iteRacj@: R₁ = {(x,y) ∈R²: x = y} ma nieskończenie wiele klas abstrakcji