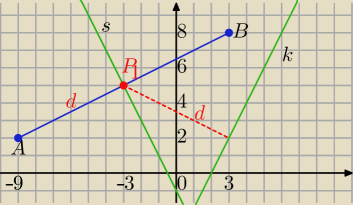
 A(−9,2), B(3,8)
k : 2x−y−4=0.
P(x,y) − punkt jednakowo odległy od p. A i B i prostej k
Wszystkie punkty jednakowo odległe od A i B leżą na symetralnej odcinka AB
1) Symetralna AB:
|PA|=|PB|
|PA|=√(−9−x)2+(2−y)2=√(x+9)2+(y−2)2
|PB|=√(x−3)2+(y−8)2
√(x+9)2+(y−2)2=√(x−3)2+(y−8)2 /2
(x+9)2+(y−2)2=(x−3)2+(y−8)2⇔
s:y=−2x−1
P=(a, −2a−1) ∊s
odległość od p. B
d=√(3−a)2+(8+2a+1)2=√(a−3)2+(2a+9)2
d=√5*√a2+6a+18
A(−9,2), B(3,8)
k : 2x−y−4=0.
P(x,y) − punkt jednakowo odległy od p. A i B i prostej k
Wszystkie punkty jednakowo odległe od A i B leżą na symetralnej odcinka AB
1) Symetralna AB:
|PA|=|PB|
|PA|=√(−9−x)2+(2−y)2=√(x+9)2+(y−2)2
|PB|=√(x−3)2+(y−8)2
√(x+9)2+(y−2)2=√(x−3)2+(y−8)2 /2
(x+9)2+(y−2)2=(x−3)2+(y−8)2⇔
s:y=−2x−1
P=(a, −2a−1) ∊s
odległość od p. B
d=√(3−a)2+(8+2a+1)2=√(a−3)2+(2a+9)2
d=√5*√a2+6a+18
| |2a−(−2a−1)−4| | ||
2)d(P,k)= | ||
| √22+12 |
| 49 | ||
stąd a=− | lub a=−3 | |
| 3 |