W prostokącie mniejszy bok ma dlugosc 6cm, a kąt ostry między przekątnymi ma mia
Krzysiek: W prostokącie mniejszy bok ma długość 6 cm, a kąt ostry między przekątnymi ma miarę 30 stopni.
Jaka jest długość promienia okręgu opisanego na tym prostokącie?
Zrobiłem to na twierdzenie cosinusów ale nie wiem dlaczego nie wychodzi z twierdzenia sinusów
może ktoś pomóc
15 sty 19:33
wredulus_pospolitus:
to pokaż co Ci wyszło i jak liczysz z tw. sinusów
15 sty 19:36
Krzysiek: Nie wychodzi z sinusów tylko nwm dlaczego przecież teoretycznie mogę dać 6/sin 30 =2R
2R=12
R=6
TYLKO źle wychodzi
15 sty 19:38
15 sty 19:41
Krzysiek: Nie rozumiem
15 sty 19:51
wredulus_pospolitus:
tw. sinusów tyczy się TRÓJKĄTA WPISANEGO w okrąg ... który trójkąt jest WPISANY w okrąg

ten
z kątem 30
o (i wierzchołkiem w środku okręgu w który niby jest wpisany) czy ten z kątem 15
o

15 sty 19:53
Eta:
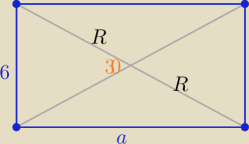
a>6
| | 1 | |
P▭= |
| *2R*2R*sin30o = R2 i P▭ =6a |
| | 2 | |
to R
2=6a ⇒ R=
√6*
√a
Z tw. Pitagorasa
a
2+6
2=(2R)
2 i R
2=6a
⇒ a
2 −24a +36=0 , Δ= 12
√3 i a>6 to a= 12+2
√3 =6(2+
√3) więc
√a=
√6*
√2+√3
R=
√6*
√6*
√2+√3
R= 6
√2+√3
===========
15 sty 20:08
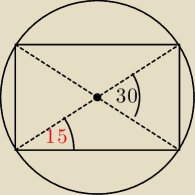 a tw. sinusów mówi o tym, że który kąt należy użyć
a tw. sinusów mówi o tym, że który kąt należy użyć 


 ten
z kątem 30o (i wierzchołkiem w środku okręgu w który niby jest wpisany) czy ten z kątem 15o
ten
z kątem 30o (i wierzchołkiem w środku okręgu w który niby jest wpisany) czy ten z kątem 15o

 a>6
a>6