Oblicz bok i wysokość Grigorij: Pole rombu wynosi 32√2 a kąt ostry 60 stopni

wredulus_pospolitus:

	h
cos 60o =
	a

P = a*h układ równań, wyznaczasz a i h

wredulus_pospolitus:

	h
tfu ... sin 60o =
	a

wredulus_pospolitus: PS. można też zauważyć, że ten romb to nic innego jak dwa trójkąty równoboczne o boku 'a'. Korzystasz z gotowych wzorów na pole i wysokość w trójkącie równobocznym

Grigorij: A mógł byś mi pomóc bo nie za bardzo mi to wychodzi

wredulus_pospolitus: to pokaż co byłeś w stanie zrobić ... bo jak na razie to jest to: "weź mi to zrób bo mi się nie chce"

Grigorij:

	a2√3
No to szukam a z wzoru P =
	4

Mnożę obustronnie przez 4 i wychodzi mi 64√2 = a²√3 i nie rozumiem co mam dalej robić

wredulus_pospolitus: dalej ... wyznacz a² ... a następnie 'a'

wredulus_pospolitus: a od kiedy 32√2 * 4 = 64√2

wredulus_pospolitus: ... no dobra ... w końcu są dwa trójkąty czyli mamy tutaj skrót myślowy

Grigorij: Co? Weź nie strasz

Mila: P_▱=32√2 1)

	a2√3
32√2=2*		/*2
	4

64√2=a²√3 /*√3 64√6=3*a²

	64√6
a2=
	3

	84√6
a=
	√3

============ 2) a*h=32√2

8*4√6
	*h=32√2 /*√3
√3

8⁴√6*h=32√6 /:8 h*⁴√6=4√6 h*⁴√6=4⁴√36

	44√36
h=
	4√6

h=⁴√6 ===========

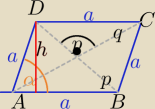
Mila: II sposób α=60^o P_ABCD=32√2 1)

	p*q
P▱=a*h lub P▱=		lub P▱=a*a*sinα w zależności co mamy dane.
	2

32√2=a²*sin60^o

	√3
32√2=a2*		/*2
	2

64√2=√3*a² /*√3 64√6=3a²

	64√6
a2=
	3

	8√√6
a=
	√3

2) a*h=32√2

8√√6
	*h=32√2 /*√3
√3

8⁴√6*h=32√6 /:8 h*⁴√6=4√6 h*⁴√6=4⁴√36

	44√36
h=
	4√6

h=⁴√6 ===========

Eta: h=4⁴√6

Mila: Zgadza się , zgubiłam czwórkę. A autor stracił już zainteresowanie.

Eta: A może pole miało być : 32√3 ?

Mila: Też tak myślę.