geometria Liceum1: 1. Uzasadnij, że spośród 65 liczb naturalnych znajduje się 9 liczb takich, że suma jest podzielna przez 9. 2. W czworokącie ABCD mamy |<DAB|=|<ABC| oraz symetralne boków AD i BC przecinają się w punkcie M leżącym na boku AB. Uzasadnij, że |AC|=|BD|. 3. W trapezie ABCD punkty M i N są odpowiednio środkami boków AB i CD oraz zachodzi równość |MN| = ¹₂(|AB|−|CD|). Wykaż, że |<BAD|+|<ABC|=90^o

Maciess: W 1. nie ma nic że mają być kolejne liczby naturalne?

wredulus_pospolitus: W 1 wystarczy zauważyć, że w zbiorze 65 dowolnych liczb naturalnych NA PEWNO znajdzie się minimum 9 takich, które mają taką samą resztę przy dzieleniu przez '9' ... oznacza to, że suma tych 9 liczb będzie podzielna przez dziewięć.

Liceum1: Czemu tak jest, że suma liczb dających taka sama resztę przy dzieleniu przez 9 jest podzielna przez 9? Np 14:9=1 reszty 5, 32:9=3 reszty 5, 14+32=46, 46:9=5 reszty 1 czyli nie dzieli się przez 9 i coś chyba nie gra?

wredulus_pospolitus: ale 9 takich liczb już będzie podzielna przez '9' mamy liczby które można zapisać w postaci: x₁ = 9a₁ + r x₂ = 9a₂ + r .... x₉ = 9a₉ + r to x₁+x₂+...+x₉ = 9(a₁+a₂+...+a₉) + 9r masz podzielność przez '9'

ABC: 1,10,19,28,37,46,55,64 2,11,20,29,38,47,56,65 3,12,21,30,39,48,57 4,13,22,31,40,49,58 5,14,23,32,41,50,59 6,15,24,33,42,51,60 7,16,25,34,43,52,61 8,17,26,35,44,53,62 9,18,27,36,45,54,63 Wredulus aż tak proste to nie jest

wredulus_pospolitus: Ach ... tam jest 65 liczb czemu ja wziąłem sobie 8*9 + 1 No dobrze ... więc popatrzmy na pesymistyczne możliwości: a) nie może być 9 liczb z tą samą resztą (bo będzie tak jak pisałem). Więc maksymalnie może być 8 liczb o jednej i tej samej reszcie. b) minimum osiem reszt musi mieć przynajmniej 7 przedstawicieli (7*8 + 8 = 64 ; 8*8 + 1 = 65) W efekcie mamy jedną z poniższych możliwości: 1) Wybieramy 7 liczb z resztą '1', jedną liczbę z resztą '2' i jedną liczbę z resztą '0' 2) Akurat jest tylko jedna liczba z resztą '1' ... no to wybieramy 7 liczb z resztą '3', jedną z resztą '2' i jedną z resztą '1'

Eta: Mogę się "wciąć" do 2/ i 3/ ?

wredulus_pospolitus: Wcinaj się wcinaj

Eta: No ..........ale nie mam nożyczek

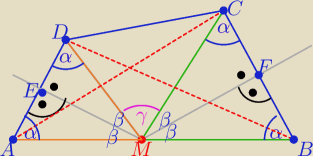
Eta: zad2/ 1/ rys. i oznaczenia.... 2/ ΔADM i MBC są równoramienne i podobne z cechy (kkk) to: |AM|=|DM| i |BM|=|CM| oraz |<AMD| =|<BMC|= 2β 3/ to ΔAMC i BMD są przystające z cechy (bkb) bo |AM|=|DM| i |BM|=|CM| i |<AMC|=|<BMD|= 2β+γ zatem |AC|=|BD| c.n.w.

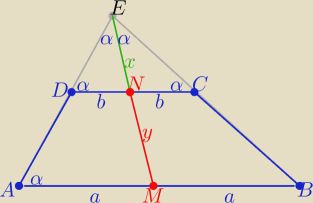
Eta: 1/ rysunek i oznaczenia 2/ przedłużamy ramiona do punktu przecięcia E w ΔABE odcinek EM=x+y i odcinek EN=x zawierają się w środkowej tego trójkąta 3/z podobieństwa ΔABE i DCE z cechy (kkk)

	2a		x+y		1
		=		i y=		(2a−2b) ⇒ y=a−b ( z treści zadania
	2b		x		2

	a		x+a−b
to		=		⇒ (a−b)x=b(a−b) ⇒ x=b
	b		x

więc Δ DNE i ΔCNE są równoramienne o kątach przy ramionach równych α to 4α=180^o ⇒ 2α=90^o = |<DEC| czyli ΔABC jest prostokątny zatem |<BAD|+|<ABC|=90^o c.n.w.

PW: Jeszcze o zadaniu 1 (trochę inna końcówka niż u wredulusa). Podzielmy zbiór 65 liczb na 9 podzbiorów (niektóre mogą być puste), przy czym w zbiorze A_k znajdą się liczby, których reszta z dzielenia przez 9 jest równa k (k=0,1,2,...,8). Jeżeli w którymś z tych zbiorów, np. A_m znajdzie się 9 elementów, to suma tych elementów 9p₁+m+9p₂+m +...+9p₉+m = 9s+9m jest podzielna przez 9. Jeżeli w każdym zbiorze jest co nawyżej 8 elementów, to z faktu że 65 = 1 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 wynika, że każdy zbiór ma co najmniej 1 element (nie może być mniej niż 1, bo wtedy istniałby składnik równy 9). Wybierając po jednym składniku z każdego zbioru otrzymamy (9p₁+0)+(9p₂+1)+(9p₃+2)+...+(9p₈+8) = 9s +(1+2+3+...+8) =

	1+8
= 9s +		8 = 9s + 9•4
	2

− sumę podzielną przez 9.