Symetria paraboli względem prostej y=-5 vedkav: Proszę o wytłumaczenie jak się przelształca parabolę przez symetrię względem prostej. Mam takie przykład: parabola: y=x²+4x−5 symetria względem y=−5

Jolanta: umiesz narysowac parabolę y=x²+4x−5 ?

the foxi: w przypadku prostych postaci y=a lub x=b, gdzie a,b∊ℛ sprawa jest prosta: w tym przykładzie y=−5 rysujesz parabolę oraz daną prostą tę część paraboli, co jest pod nią, odbijasz symetrycznie nad nią a tę, która była nad prostą − odbijasz pod tę prostą

Jolanta: Póżno jest ,umiesz czy nie ?

Jolanta: to parabola y=x² przesunieta liczymy jej wierzchołek W(p.q)

	−b
p=		=U{−4}{2*1)=−2
	2a

	−Δ
q=		Δ=b2−4ac=42−(4*(−5))=36
	4a

	−36
q=		=−9
	4*1

policzymy w tórym miejscu przecina oś x

	−b−√Δ		−4−6
x1=		=		=−5
	2a		2

	−b+√Δ		−4+6
x2=		=		=1
	2a		2

teraz układ wspólrzednych zaznaczassz wierzchołek x₁,x₂ rysujesz parabole

Jolanta: po lewej stronie kliknij funkcja kwdratowa tam masz wiadomości po narysowaniu paraboli rysujesz prosta rownoległa do osi x tak zeby przecinała os y w punkcie −5 i dalej jak napisal the foxi

Eta:

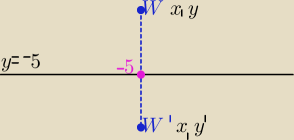
	y+y'
W'(x , 2*(−5) −y) bo		=−5
	2

y=x²+4x−5 = (x²+4x+4)−9 = (x+2)²−9 W( −2, −9) to W^' (−2, 2*(−5)+9) = (−2,−1) y= −(x+2)²−1 bo parabola ramionami do dołu ===========

vedkav: Jolanta pewnie, że umiem, w taki sposób z rysowaniem bym sobie poradziła, dziękuję Ci za odpowiedź, chodziło mi właśnie o ten sposób, który przedstawiła Eta, dzięki wszystkim

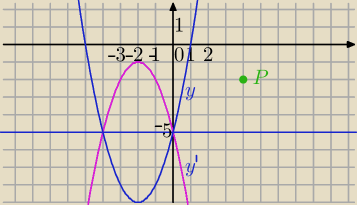
Mila: III sposób P(x,y) −dowolny punkt P'(x',y') punkt symetryczny do P względem prostej y=−5 S(x,−5) środek odcinka PP' x=x'⇔

	y+y'
−5=		⇔ y=−10−y'
	2

y=x²+4x−5 (−10−y')=x'²+4x'−5 −y'=x'²+4x'+5 y'=−x'²−4x'−5 Opuszczamy "znaczki" y=−x²−4x−5 ===========