Równanie Filip: Wyznacz wszystkie wartości parametru a, dla których równanie (cox+a)(sin²x−a)=0 ma w przedziale <0;2π> dokładnie trzy różne rozwiązania

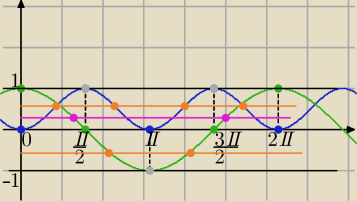
Eta: cosx=−a v sin²x=a i x∊<0.2π> rozpatrujemy : dla a∊(−∞, −1) U(1,∞) −−− brak rozwiązań w obydwu równaniach dla a∊(0,1) cosx= −a 2 rozwiązania sin²x=a −−− 4 rozwiązania dla a∊(−1,0) cosx= −a 2 rozwiązania sin²x=a −−− brak rozwiązań bo a ujemne dla a=0 cosx= 0−− 2 rozwiązania sin²x=0 3 rozwiązania dla a= −1 cosx= 1 −− 2 rozwiązania sin²x= −1 −− sprzeczne dla a= 1 cosx= −1 −−1 rozwiązanie sin²x= 1 −−− 2 rozwiązania zatem tylko dla a= 1 są trzy różne rozwiązania : {π/2 , π, 3π/2}