trójkąt mat-fiz: Dwusieczna kąta ACB trójkąta ABC przecina bok AB w punkcie D oraz symetralna odcinka CD dwusiecznej przecina prostą AB w punkcie M Wykaż,że |MA|/|MB| = |AC|²/|BC|²

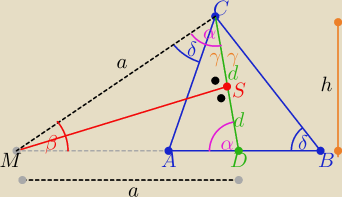
Eta: To może tak : 1/ rys. .... i oznaczenia 2/ dorysowujemy odcinek MC więc ΔMDC jest równoramienny bo MS jest symetralną i wysokością ΔMDC zatem kąty MDC i MCD mają miary α 3/ W ΔAMC δ= α−γ to α=γ+δ ⇒ że w ΔBDC |<DBC|=δ zatem trójkąty AMC i MBC są podobne z cechy (kkk) (δ i β ) −− wspólne miary

	|AC|
w skali k=
	|BC|

	|MA|*h
to ich pola są w stosunku		= k2 ⇒ teza
	|MB|*h

|MA|		|AC|		|AC|2
	= (		)2 =
|MB|		|BC|		|BC|2

c.n.w.

Eta: Może Mila poda jeszcze inny sposób