stół okrągły kkkleopatrakkk: Kombinatoryka. Okrągły stół. Przy okrągłym stole ustawiono 6 jednakowych krzeseł. Na ile sposobów może usiąść przy tym stole 6 osób, tak, aby osoby A i B usiadły naprzeciwko siebie? Wyszło mi 48, bo 2*4! jest jedno rozstawienie takie, że A i B siedzą naprzeciwko siebie, gdyż jest to okrągły stół, więc przesuwanie np. o 1 w krzesło całego towarzystwa jest tu nadal uznawane jako to samo, wyjściowe rozstawienie, a cała reszta może sobie zasiąść na 4! sposobów, a tę dwójkę wziąłem stąd, że przecież A i B mają takie samo prawo zamienić się miejscami jak np C z D albo E z F (a to przecież opisujemy pisząc 4!)

kkkleopatrakkk: tymczasem odp to 24, czyli 4!

Pytający: "jest jedno rozstawienie takie, że A i B siedzą naprzeciwko siebie" "a tę dwójkę wziąłem stąd, że przecież A i B mają takie samo prawo zamienić się miejscami jak np C z D albo E z F" To w końcu na ile sposobów A i B mogą usiąść naprzeciwko siebie? Musisz ustalić jakiś punkt odniesienia przy tym stole, znaczy rozsadzać względem jakiejś osoby (skoro krzesła są nierozróżnialne). Przykładowo: • przy stole siedzi A (punkt odniesienia), wtedy B może dosiąść się na 1 sposób (naprzeciwko A), a pozostali na 4! sposobów; łącznie 1*4!=4! • przy stole siedzi C (punkt odniesienia), wtedy A może dosiąść się na 4 sposoby (nie naprzeciwko C), B na 1 sposobów naprzeciwko A, a pozostali na 3! sposobów; łącznie 1*4*3!=4! W jakiejkolwiek kolejności będziesz rozsadzał i tak wyjdzie 4! sposobów.

wredulus_pospolitus: Na 4! sposobów rozwiązanie: 1) osoba A siada na 'dowolnym' miejscu (1 możliwość) 2) osoba B siada na przeciwko (1 możliwość) A 3) pozostałe osoby zajmują kolejne miejsca na 4,3,2 i w końcu 1 sposób stąd: 1*1*4! = 4! Koooniec

Jerzy: Kluczowe słowo: „jednakowych” krzeseł (czytaj :żadne nie jest wyróżnione kolorem lub numerem)

kkkleopatrakkk: Nadal nie wiem czemu nie moga sie zamienic miejscami

kkkleopatrakkk: @Jerzy no tak, ale to nie jest tak, że w okrągłym stole to wszystko sprowadza się do punktu odniesienia? a przy okragłym stole jedyny punkt odniesienia to sasiedzi. Jeśli sąsiedzi się zmieniają, to znaczy, że zmieniliśmy rozstawienie. A "A" zmieni swoich sąsiadów tak samo jak i osoba "B" zmieni swoich jeśli zamienimy A i B miejscami.

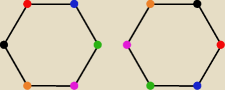
wredulus_pospolitus: Skoro stół jest okrągły i krzesła są JEDNAKOWE to pierwsza siadająca osoba siada na 'nierozróżnialnej' pozycji, bo każde miejsce jest TAKIE SAMO Kolejne osoby już siadają na konkretnych miejscach (bo punktem odniesienia jest ta pierwsza osoba która usiadła). Innymi słowy −−− powyższe dwa rysunki przedstawiają TO SAMO usadzenie

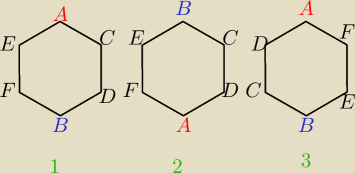
wredulus_pospolitus: Zauważ, że w 4! masz przetasowania ludzi C,D,E,F uwzględnione ... chcesz jeszcze uwzględnić 'przesiadanie się A z B' no to popatrz na rysunki 1) Masz taki układ i teraz chcesz zamienić A z B miejscami (2) i uważasz że ten układ jeszcze nie był liczony ... otóż był ... tutaj (3)

wredulus_pospolitus: przesadzając 'A' "przesadzasz" układ odniesienia

kkkleopatrakkk: Dzięki. Dzięki rysunkom wszystko jasno widać. Ale dlaczego w podpunkcie a) (osoby A i B siedzą obok siebie) tym razem zamiana będzie uwzględniana? Dlaczego nie jest tutaj analogicznie?

wredulus_pospolitus: Ponieważ B może siedzieć 'na prawo' od A bądź 'na lewo' od A (dwie możliwości)

wredulus_pospolitus: zauważ, że to 'A' jest punktem odniesienia i wokół niego 'wszystko się kręci'

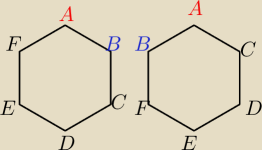
wredulus_pospolitus: Zauważ, że układ (1) i (2) różnią się tym po której stronie (względem A) siedzi B ... tego drugiego układu nie da się 'powtórzyć' mając układ (1) i tylko zmieniając usadzenie osoby C−F.

kkkleopatrakkk: Czyli mimo, że stół jest okrągły, to nie zawsze nie−nie liczymy zamiany miejsc... Jakieś te zadanka są mało intuicyjne

Pytający: Jak najbardziej intuicyjne, przecież przy tym stole miejsca: trzecie na prawo i trzecie na lewo to jedno i to samo miejsce... to naprzeciwko, natomiast pierwsze na lewo i pierwsze na prawo to już dwa różne miejsca (wszystko oczywiście względem miejsca będącego punktem odneisienia).

wredulus_pospolitus: Mało intuicyjne? Siada A ... i na ilu miejscach może usiąść B, aby siedzieć obok niego? Na dwa (po lewej od A albo po prawej od A) A na ilu aby siedzieć NAPRZECIWKO? Na jeden (bo tylko jedno miejsce jest na przeciwko A). A na ilu aby pomiędzy nimi była jedna osoba? Na dwa (dwa miejsca na lewo albo na prawo od A). Co tutaj jest mało intuicyjne

kkkleopatrakkk: Czyli idąc tym tokiem myślenia, w ppkt. "tylko osoba c siedzi między a i b" − Sadzam osobę A na jakimkolwiek miejscu − osobę C mogę dać 1 miejsce na lewo od A, wtedy daję B na 2 miejsca na lewo od A, lub osobę C mogę dać 1 miejsce na prawo od A, wtedy daję osobę B na dwa miejsca na prawo od A. − w obu przypadkach reszta towarzystwa może zająć krzesła na 3! sposobów Czyli rozwiązaniem będzie : 2*3!=12 ?

kkkleopatrakkk: W sumie to są logiczne te zadania, moim błędem było to, ze tę 2 traktowałem jako zamianę miejsc A z B a tu jeśli dobrze rozumiem, 2 powinna być traktowana jako możliwość usadzeń drugoplanowej osoby w zadaniu względem tej A

Bleee: Dokładnie. Ponieważ A jest naszym punktem odniesienia i jego przesadzanie kompletnie nic nie zmienia bo to on tworzy punkt odniesienia dla całego układu.