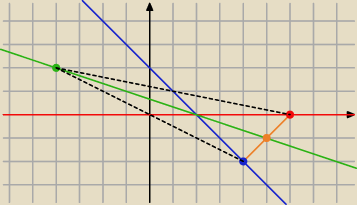
 1) Należy zauważyć, że środkowe przecinają się w jednym punkcie, stąd trzecia środkowa będzie
dana równaniem
2) Ponadto, wiemy że środek ciężkości dzieli środkową w proporcji 2:1. Stąd wyznaczamy punkt w
na przeciwko znanego nam wierzchołka
3) Teraz należy wyznaczyć jaka prosta będzie zawierać bok tego trójkąta, na który była
opuszczona ta środkowa (pomyśl w jaki sposób to zrobić)
4) Przecięcie tejże prostej z dwoma podanymi w zadaniu środkowymi daje nam współrzędne dwóch
pozostałych wierzchołków
1) Należy zauważyć, że środkowe przecinają się w jednym punkcie, stąd trzecia środkowa będzie
dana równaniem
2) Ponadto, wiemy że środek ciężkości dzieli środkową w proporcji 2:1. Stąd wyznaczamy punkt w
na przeciwko znanego nam wierzchołka
3) Teraz należy wyznaczyć jaka prosta będzie zawierać bok tego trójkąta, na który była
opuszczona ta środkowa (pomyśl w jaki sposób to zrobić)
4) Przecięcie tejże prostej z dwoma podanymi w zadaniu środkowymi daje nam współrzędne dwóch
pozostałych wierzchołków

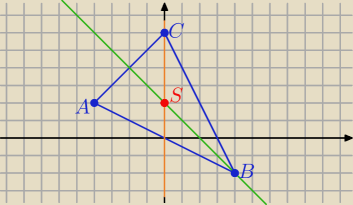 S −−− jest środkiem ciężkości trójkąta ( bo jest punktem przecięcia środkowych)
S −−− jest środkiem ciężkości trójkąta ( bo jest punktem przecięcia środkowych)
| xA+xB+xC | yA+yB+yC | |||
(**) S( | , | ) −−− wzór jest w karcie wzorów | ||
| 3 | 3 |
| 0+x−4 | b−x+2+2 | |||
=0 ⇒ x= 4 i | =2 ⇒ b=6 | |||
| 3 | 3 |

