Próbna Maciess: Ma ktoś wczorajszy arkusz próbnej z nowej ery?

iteRacj@: W zeszłym roku opublikowali po ∼miesiącu.

Maciess: Dany jest trójkąt ABC o polu 5, gdzie A=(5,3) B=(1,0). Prosta y=2x−7 zawiera wysokość trójkąta. Wyznacz C. Robię rysunek i od razu widzę to C=(3,−1).Jak zacząłem liczyć to wyszły jakieś śmieszne rzeczy. Ktoś pokaże jakies zgrabne rozwiązanie?

kama: zaznaczam, ale nie wiem czy dobrze ja bym wykombinowała tak. 1.zauważyłam że punkt A należy do prostej y=2x−7 2. czyli AC to będzie h 3.stąd prosta prostopadła do prostej ac przechodząca przez punkt B i wyszło mi miejsce przecięcia czyli C (3, −1) pewnie źle wymyśliłam bo nie użyłam pola ciekawe jak można inaczej ?

ABC:

	1		1
prostopadłą do y=2x−7 przechodząca przez (1,0) ma równanie y=−		x+		, na tej prostej
	2		2

leży C, podstawić do wzoru na pole trójkąta zbudowanego na dwóch wektorach

kama: no właśnie czy to pole jest konieczne?Bo mi wyszły współrzędne ok tylko zauważyłam że punkt należy do prostej.

ABC: jest konieczne bo to co ty napisałaś w pkt 2 nie musi być prawdą, to tylko gdy trójkąt jest prostokątny, tutaj mogą być 2 rozwiązania trzeba policzyć

kama: Tak już sobie to zrobiłam i wiem.

Maciess:

	1		1
C=(x,−		x+		)
	2		2

	1
P=		d(BA,BC) // wektory
	2

	1		1
BA=[4,3] BC=[x−1,−		x+		]
	2		2

|4 3|

	1		1
|x−1 −		x+		| d(BA,BC)=−2x+2−3x+3=−5x+5
	2		2

	1
P=		(−5x+5)
	2

10=−5x+5 ⇒x=−1 C=(−1,1) Wydaje mi sie ze cos skopałem

ABC: kolego a gdzie wartość bezwzględna we wzorze ? pisałem coś o dwóch rozwiązaniach...

Maciess: Gdzie powinienem nałozyć moduł? Nie korzystałem nigdy wczesniej z tej metody

ABC: popatrz tu: https://eszkola.pl/matematyka/pole-trojkata-w-geometrii-analitycznej-5500.html

Maciess: Wszystko jasne, dziękuje

Maciess: Kolejne zadanie z próbnej. W pudełku znajduje się sto kul ponumerowanych liczbami od 1 do 100. Wylosowanie kazdej z kul jest jednakowo prawdopodobne. Wylosowano jednocześnie pięć kul. Wyznacz prawdopodobieństwo, że numery wylosowanych kul ustawione w odpowiedniej kolejnosci tworza ściśle rosnący ciąg geometryczny o całkowitym ilorazie

	100 5
|Ω|=

Licze ile jest ciągów spełniających warunek. W zależności od pierwszej cyfry 1) − druga cyfra z {2,3} więc 1*2*1*1*1=2 2) {4} 3) {6} ... 7) ∅ |A|=2+1+1+1+1+1=7

	7
P(A)=
	100 5

Poprawnie?

Mila: Nie. (x₁,x₁*q,x₁*q²,x₁q³, x₁q⁴) x₁*q⁴≤100 licz dla q=2,3,4,.

Maciess: 4⁴=256 3⁴=81 czyli tylko dla jedynki

Mila: To znaczy jeden ciąg, gdy q=3

Maciess: 1,2,4,8,16 1,3,9,27,81 2,4,8,16,32 3,6,12,24,48 4,8,16,32,64 5,10,20,40,80 6,12,24,48,96 No i tyle wg mnie

Mila: Chyba to wszystkie. Może Eta dołączy do naszego liczenia?

Maciess: Dany jest trapez ABCD w którym kąty ABC i BCD są proste. ∡DAB=60^o |AB|=2 a |BD|=√3. Oblicz |AC|.

	√19
Mój wynik |AC|=
	2

Może ktoś sprawdzic?

Eta: Ok

Maciess:

h
	=tg(60o) ⇒h=√3x
x

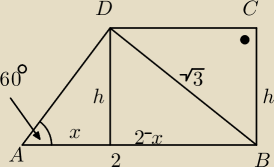
h²=3−(2−x)² h²=−x²+4x−1 3x²=−x²+4x−1 4x²−4x+1=0

	1
(2x−1)2=0 ⇒x=
	2

	√3
h=
	2

	3		19
|AC|2=22+h2=4+		=
	4		4

	√19
|AC|=
	2

Maciess: Jest jakis szybszy sposób?

Maciess:

	sin2 α		tg α
Wykaż, że jeśli α,β,γ są kątami trójkąta i zachodzi równość		=
	sin2 β		tg β

to α=β lub γ=90^o. Tu nie wiem co robic, nie robiłem dowodów jeszcze.

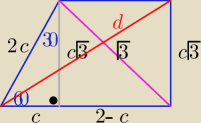
Eta: (2−c)²+(c√3)²=(√3)² i c ∊(0,2) 4c²−4c+1=0 ⇒(2c−1)²=0 ⇒ c=1/2

	3		√19
d=√4+		⇒ d=
	4		2

Maciess: @Eta a mogłabyś pomóc z tym dowodem?

Eta: zad z 18:42 1 sposób

	a		b		sin2α		a2
z tw. sinusów		= sinα i		=sinβ to		=
	2R		2R		sin2β		b2

	b2+c2−a2		a2+c2−b2
i z tw. cosinusów cosα=		i cosβ=
	2bc		2ac

	a2		sinα		cosβ
L=		i P=		*
	b2		cosα		sinβ

	a		cosβ		a		a2+c2−b2		2bc
P=		*		=		*		*
	b		cosα		b		2ac		b2+c2−a2

to a²(b²+c²−a²)=b²(a²+c²−b²) ........................... (a²−b²)(a²+b²−c²)=0 to a=b −−− trójkąt równoramienny α=β lub a²+b²=c² −− trójkąt prostokątny γ= 90^o c.n.w.

Maciess: Dziękuje

Eta:

Mila: II sposób α+β+γ=180, sinβ≠0 i cosα≠0 i cosβ≠0

sin2α		sinα		cosβ		sinβ
	=		*		/*
sin2β		cosα		sinβ		sinα

sinα		cosβ
	−		=0⇔sinα*cosα=sinβ*cosβ
sinβ		cosα

sin2α−sin2β=0⇔

	2α+2β		2α−2β
2*cos		*sin		=0
	2		2

cos(α+β)=0 lub sin(α−β)=0

	π		π
α+β=		⇔γ=		Δ jest prostokątny
	2		2

lub α−β=0 ⇔α=β Δ jest równoramienny cnw ====================

Eta: Ładnie można jeszcze tak uprościć obliczenia sin(2α)−sin(2β)=0 sin(2α)=sin(2β) ⇒ 2α=2β lub 2α= π−2β α=β lub α+β= π/2

Mila: Też myślałam o tym, ale wybrałam rozkład na iloczyn.

Eta: No to Maciess ma dwa sposoby ( z kątami i z bokami)