Równanie kwadratowe z parametrem. cardi bardi : Wyznacz wszystkie wartości parametru m, dla których mniejszy pierwiastek równania (m−2)x²+(2m+1)x+1=0 jest mniejszy od 1, ale większy pierwiastek tego równania jest większy od 2. Podałby mi ktoś warunki? Oprócz tego, że m≠2 i Δ>0.

wredulus_pospolitus: dodatkowo: f(x) = (m−2)x² + (2m+1)x + 1 1) dla m>2 f(1) < 0 f(2) < 0 2) dla m<2 f(1) > 0 f(2) > 0

cardi bardi : Wytłumaczyłbyś dlaczego akurat tak? Nie do końca chyba rozumiem:(

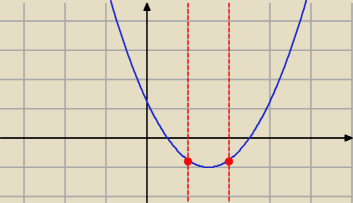
wredulus_pospolitus: Skoro chcemy aby pierwiastki tego równania były 'poza' przedziałem <1,2> to musi być taka sytuacja (rysunek dla m>2, czyli a>0, czyli ramiona skierowane do góry) Zauważ, że jeżeli wiesz, że są dwa pierwiastki (warunek dla Δ) jeżeli f(c) < 0 oznacza, że jeden z pierwiastków będzie mniejszy od c, a drugi większy natomiast warunek: f(c) < 0 oraz f(c+1) < 0 ... oznacza że: jeden z pierwiastków jest mniejszy od c i jest mniejszy od c+1 (czyli jest mniejszy od c) drugi z pierwiastków jest większy od c i jest większy od c+1 (czyli jest większy od c+1) czyli dokładnie to o co chodzi w zadaniu Analogiczny rysunek dla m<2

Maciess: Najwięcej powie ci tutaj rysunek. Zrób sobie dwie sytuacje (ramiona paraboli w góre i w dół) i coś zobaczysz

wredulus_pospolitus: zauważ dodatkowo, że podane warunku na np. wierzchołek tejże paraboli nie jest dobrym pomysłem, ponieważ: 1) można stworzyć takie parabole których wierzchołek będzie w przedziale <1,2> oraz przynajmniej jedno miejsce zerowe w tym przedziale będzie 2) można stworzyć takie parabole których wierzchołek będzie poza przedziałem <1,2> a oba miejsca zerowe będą spełniać wytyczne zadania.

cardi bardi : Dziękuję Ci bardzo!