romb matue: bardzo prosze o pomoc w rombie ABCD którego pole jest równe 10, dane są przeciwległe wierzchołki A(1,1) B(3,5). wyznacz pozostałe współrzędne wierzvhołków doszłam do wyznaczenia prostej BD która wynosi y=−1/2x +4 długość odcinka DS= √5 dlatego układam równanie na długość odcinka DS=√ (x−2)² + (y−3)² = √5 i dalej już nie wiem bo mi nie wychodzi, proszę o dokładne obliczenia z góry dziękuję

wredulus_pospolitus: 1) skoro masz podane wierzchołków A i B to znasz długość boku tegoż rombu (wyznacz także równanie prostej zawierającej AB) 2) więc znasz 'wysokość' rombu (wysokość będzie dla nas odległością prostej zawierającej CD równoległej do prostej zawierającej odcinek AB) 3) piszesz równanie okręgu o środku w punkcie A i promieniu |AB| ... sprawdzasz kiedy się 'przetnie' z prostą wyznaczoną w punkcie (2) 4) masz wyznaczone współrzędne wierzchołka C, wyznaczenie D już chyba będzie banalne (zwłaszcza że wiesz na jakiej (2) prostej leży ów punkt i o ile jest oddalony od C)

matue: niestety nic nie rozumiem z tego co piszesz

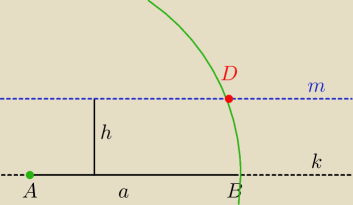
wredulus_pospolitus: 10 = |AB|*h = a*h −> h = √5 wyznaczasz prostą 'k' wyznaczasz prostą 'm' która jest równoległa to 'k' i przesunięta dokładnie o h = √5 wyznaczasz równanie okręgu o środku w A i promieniu równym |AB| punkt przecięcia się prostej 'm' z tymże okręgiem daje wierzchołek D pozostaje wyznaczyć wierzchołek C który będzie oddalony od wierzchołka D o dokładnie |AB| = 2√5 i leży on na prostej m

wredulus_pospolitus: a teraz już rozumiesz

matue: tak dziękuję bardzo

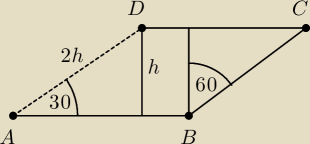
wredulus_pospolitus: Inny sposób który jest możliwy ze względu na DANE

	1
Zauważasz, że h =		|AB|
	2

więc masz sytuację jak na rysunku ... pytanie czy będzie Ci łatwo wyznaczyć punkty D i C ... osobiście, nie sądzę aby to było łatwiejsze rozwiązanie

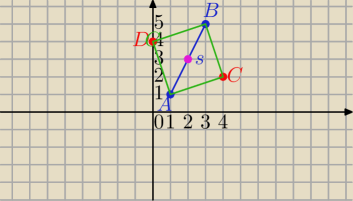
Mila: A(1,1) B(3,5)− przeciwległe wierzchołki 1) S=(2, 3)− środek AB |AB|=√2²+4²=2√5 P=10

2√5*x
	=10
2

x=2√5 Przekątne są prostopadłe, ponadto równe ⇔ czworokąt jest kwadratem. 2)SB^→=[1,2] SC^→⊥SB^→ i równej długości⇔ SC^→=[2,−1] lub [−2,1] S(2,3)→T_[2,−1]⇒C=(2+2,3−1) C=(4,2) S(2,3)→T_[−2,1]⇒D=(2−2,3+1) D=(0,4)

wredulus_pospolitus: Miluś ... a o kiedy tak oznaczamy wierzchołki czworokąta ABCD PS. Też na początku myślałem, że to będzie zadanie na pojechanie po przekątnych

Mila: No taka jest treść! Wiem, że inaczej się oznacza. Może , źle przepisał zadanie, trzeba by wiedzieć skąd to zadanie. Jakoś autorka milczy

Mila: Może były podane punkty A i C?