Stereometria maturalne
Dango: W ostrosłupie ABCS podstawa ABC jest trójkątem równoramiennym o ramionach AC I BC
długości 4 i kącie między nimi 30 stopni. Punkt E− środek krawędzi AB− jest spodkiem
wysokości tego ostrosłupa, a krawędź boczna CS tworzy z podstawą kąt 60 stopni.
Ostrosłup przecięto płaszczyzną przechodzącą przez krawędź AB i mającą
z przeciwległą krawędzią boczną CS wspólny punkt D. Oblicz pole otrzymanego przekroju,
wiedząć że z podstawą ostrosłupa tworzy on kąt 75 stopni. Prosilbym o jasne wytlumaczenie
bo nie mielismy jeszcze zaawansowanej stereometrii a juz za chwilę maturka próbna :0
8 sty 11:52
Mila:
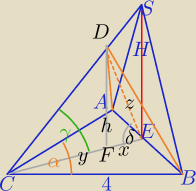
1) α=30
o, γ=60
o,δ=75
o
W ΔABC:
|AB|
2=4
2+4
2−2*4*4 cos 30
o
|AB|=4*
√2−√3
|AE|=2
√2−√3
|CE|
2+|AE|
2=4
2
|CE|
2=16−4*(2−
√3⇔|CE|
2=8+4
√3
|CE|=2
√2+√3
2)
WΔCED:
x+y=2*
√2+√3, y=2
√2+√3−x
h=x*tg75 i h=y*tg60
x*tg75=y*
√3
x*(2+
√3)=y*
√3
x*(2+
√3)=
√3*(2
√2+√3−x)
2x+
√3*x=2
√3√2+√3−
√3x
2x+2
√3x=2
√3√2+√3
2x*(1+
√3)=2
√3√2+√3
3) W ΔDFE:
| | √3*√2+√3 | | 4 | | 4√3*√2+√3 | |
z= |
| * |
| = |
| |
| | 1+√3 | | √6−√2 | | 2√2 | |
z=
√6*
√2+√3
4)
| | 1 | |
PΔABD= |
| *4*√2−√3*√6*√2+√3 |
| | 2 | |
P
ΔABD=2
√6
=================
8 sty 23:16
 1) α=30o, γ=60o,δ=75o
W ΔABC:
|AB|2=42+42−2*4*4 cos 30o
|AB|=4*√2−√3
|AE|=2√2−√3
|CE|2+|AE|2=42
|CE|2=16−4*(2−√3⇔|CE|2=8+4√3
|CE|=2√2+√3
2)
WΔCED:
x+y=2*√2+√3, y=2√2+√3−x
1) α=30o, γ=60o,δ=75o
W ΔABC:
|AB|2=42+42−2*4*4 cos 30o
|AB|=4*√2−√3
|AE|=2√2−√3
|CE|2+|AE|2=42
|CE|2=16−4*(2−√3⇔|CE|2=8+4√3
|CE|=2√2+√3
2)
WΔCED:
x+y=2*√2+√3, y=2√2+√3−x