fizgura kacper: Dane s¡ punkty na plaszczyznie: A(0, 0), B(2, 0) i C(0, 2). Niech S bedzie zbiorem takich punktów D na plaszczyznie, dla których oba trójk¡ty ABD i ACD s¡ jednoczesnie rozwartokatne i ich odleglosc od punktu A nie przekracza 2. Oblicz pole figury S.

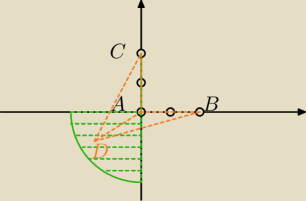
iteRacj@: Rozumiem, że to odległość punktu D od punktu A nie przekracza 2.

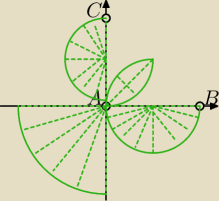
ite: Po dalszych poszukiwaniach znajduję taki zbiór punktów spełniających warunki zadania.

kacper: Ten kawałek z pierwszego rysunku tak, ten w 1 cwiartce chyba też ale te 2 polkola chyba nie pasują... Tam będzie kat prosty

iteRacj@: Te półkola bez krawędzi (półokręgów), tylko ich wnętrza, tam kąt jest rozwarty. Ale nie miałam jak zaznaczyć, że tylko wnętrze. W tej soczewce tak samo tylko wnętrze.

Mila: Śliczne rysuneczki

iteRacj@: ten drugi = duszek w sukni i ze skrzydełkami

kacper: Ok dziękuję bardzo, a pomożesz jeszcze z polem?

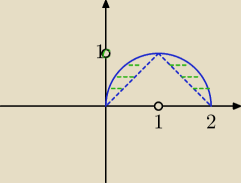
iteRacj@: obliczenie pól części kół nie stanowi problemu, ta soczewka z I ćwiartki ma takie samo pole jak różnica półkola i trójkąta z tego rysunku