Ciągi kasia: Dobry wieczór. 1) Jeśli ciąg jest zbieżny to jest ograniczony. A czy jeżeli ciąg jest ograniczony to wystarczy, aby był zbieżny? I ciąg, aby był zbieżny może, ale nie musi, być monotoniczny, zgadza się?

	pi		2
2) Jeżeli mam szereg ∑ 2n *		= ∑ (		)n * pi i tutaj pojawia się moje pytanie.
	3n		3

Czy pi mogłabym wyciągnąć przed sumę? Bo stała chyba nie ma wpływu na zbieżność?

	n5
3) ∑		czy zbieżność tego szeregu mogę ustalić z kryterium d'Alamberta lub
	2n

Cauchy'ego?

	1
4) ∑		jest zbieżny, zgadza się?
	n!

5) Jeżeli z kryterium Cauchy'ego wychodzi, że szereg jest zbieżny, to czy od razu mogę stwierdzić, że jest zbieżny bezwzględnie? (trafiło mi się kilka przykładów, że sprawdzając tym kryterium od razu wychodziły mi te dwie 'zbieżności', zastanawiam się czy tak jest zawsze?) Wiem, że to sporo pytań. Będę bardzo wdzięczna, jeśli ktoś zechce poświęcić swój czas. Pozdrawiam.

ICSP: 1) zbieżny ⇒ ograniczony ograniczony (nie ⇒) zbieżny ograniczony i monotoniczny ⇒ zbieżny 2) możesz 3) tak 4) tak do e 5) jeśli dobrze pamiętam kryterium Cauchego stosujemy dla szeregów o wyrazach nieujemnych. Takie szeregi jeżeli są zbieżne to są zbieżne bezwzględnie

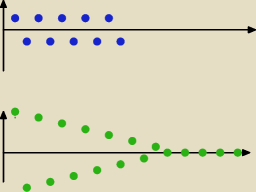
iteRacj@: czy jeżeli ciąg jest ograniczony to wystarczy, aby był zbieżny? nie I ciąg, aby był zbieżny może, ale nie musi, być monotoniczny, zgadza się? tak

kasia: Pięknie dziękuję! Kryterium Cauchy'ego zostało nam przedstawione tak: lim_n→∞ ⁿ√|a_n| : a) >1 rozbieżny, b)<1 zbieżny. Nic o wyrazach a_n nie było wspomniane. Tylko jest wartość bezwzględna pod pierwiastkiem.

Adamm: To nie do końca to co nazywamy zazwyczaj kryterium Cauchy'ego, tylko jego wariacja, ale tak, wtedy jest zbieżność bezwzględna dodatkowo, lim można zastąpić przez lim sup

kasia: Dziękuję!