Wyznaczyć przedziały monotonicznosci Oliwia: Wyznaczyć przedziały monotonicznosci a) x²+1/x² czyli dziedzina to R/{0} pochodna 2x−1/x³ i nie wiem co dalej prosze o pomoc

jc: Minima w punktach ±1. Naszkicuj wykres i wszystko stanie się jasne.

Oliwia: no mz x(2−2/x⁴) czyli x=0 i 2−2/x⁴=0 x=1 lub x=−1 tak? ale co z zerem nie nalezy do dziedziny czyli nie bierzemy go pod uwage tak?

jc: Nie bierzemy ...

Oliwia: (−∞,−1) (1,∞) funkcja malejaca (−1,1) funkcja rosnaca?

PW: Bez pochodnych − jak w liceum.

	1
f(x) = x2+		jest funkcją parzystą, wystarczy więc zbadać ją dla x∊(0,∞).
	x2

Niech x₂>x₁>0.

	1		1
f(x2)−f(x1) = x22+		− (x12+		) =
	x22		x12

	(x1−x2)(x1+x2)
=(x2−x1)(x2+x1)+		=
	x1x2

	1
= (x2−x1)((x2+x1)(1−		).
	x1x2

Widać więc, że f(x₂)−f(x₁) ma taki znak jak

	1		x1x2−1
1−		=		,
	x1x2		x1x2

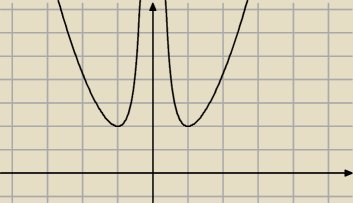
czyli taki znak jak x₁x₂ − 1, x₁, x₂ > 0. Jest oczywiste, że: − jeżeli x₁, x₂ ∊ (0, 1), to f(x₂)−f(x₁) < 0 − jeżeli x₁, x₂ ∊ <1,∞), to f(x₂) − f(x₁) > 0. Oznacza to, że funkcja f jest malejąca na przedziale (0, 1) i rosnąca na przedziale <1,∞), czyli w punkcie x₀=1 osiaga minimum. Zastosowanie parzystości pozwala stwierdzić, że minimum jest także w punkcie (−1). Przedziały monotoniczności to (−∞, −1) (malejąca) oraz (−1, 0) (rosnąca).

PW:

Oliwia: w liceum niestety tego nie mialam a po drugie musze na kolokwium policzyc to z pochodnej

PW: Ale nie pisz takich rzeczy jak o 17:07, bo po pierwsze nie wiadomo co ma znaczyć napis (−∞,−1) (1,∞) funkcja malejąca, a po drugie jest malejaca tylko na jednym z tych przedziałów. nie wolno było napisać, że f jest rosnąca na (−1, 1), bo w tym przedziale jest "dziura" − do dziedziny nie należy 0. Twierdzenie − warunek dostateczny monotoniczności funkcji − działa tylko na przedziale "bez dziur" − sprawdź założenia twierdzenia.

Oliwia: Racja przecież zera nie biorę wcale pod uwage dziękuje bardzo juz rozumiem