Geometria analityczna nvm: 1. Dane są punkty A(−1,4) B(7,−1). Wyznacz na paraboli y=x² taki punkt C, dla którego P△=15 2. Odcinek AB o końcach A(8,−2) B(−8,6) jest przeciwprostokątną trójkąta prostokątnego ABC. Spodek wysokości D poprowadzonej z wierzchołka C dzieli przeciwprostokątną AB na takie AD i DB że |AD|DB|=5:3. Wyznacz współrzędne wierzchołka C 3. Trójkąt ABC jest trójkątem prostokątnym równoramiennym, w którym |AB|=|AC|. Bok AB zawiera się w prostej k: x+2y−9=0, a C(4,10). Obrazem △ABC w jednokładności o środku S i ujemnej skali k jest △A1B1C1, którego P=5⁵₈. Przyjmując że A1(−2, −6¹₂), wyznacz współrzędne środka S tej jednokładności i skalę k Za rozwiązania bardzo dziękuję!

iteRacj@: 1/ A=(−1,4) B=(7,−1) C=(x_c, x_c²) AB^→=B−A=[7−(−1), (−1)−4]=[8, −5] AC^→=C−A=[x_c−(−1), x_c²−4]=[x_c+1, x_c²−4]

	1		1		8 −5 xc+1 xc2−4
P=		|det(AB→,AC→)|=				← te nawiasy mają być
	2		2

równoległe (wyznacznik)

	1
P=		[8(xc2−4)−(−5)(xc+1)]=15
	2

z tego równania wylicz x_c

iteRacj@: wyjaśnienie wzoru na pole trójkąta w układzie współrzędnych było niedawno na forum http://www.maturzysta.info/pdf_portal/poletrojkata_wxoyx.pdf metoda IV − najkrótsza

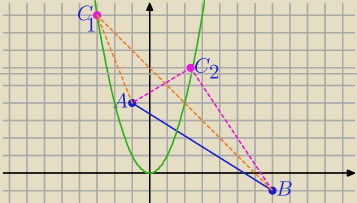
xoy: 1) |AB|=√8²+5²=√89

	1
PΔABC=15⇔15=		*√89*h
	2

	30
h=
	√89

C=(c,c²)∊wykresu y=x² odległość punktu C od prostej AB jest równa U{30}{√89. 2) Prosta AB:

	5		27
y=−		x+		/*8
	8		8

−5x−8y+27=0 k: 5x+8y−27=0

	|5c+8*c2−27|		30
d(C,k)=		=		⇔
	√52+82		√89

|5c+8c²−27|=30

	19
c=−3 lub c=
	8

	19		361
C=(−3,9) lub C=(		,		)
	8		64

========================

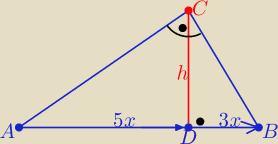
Eta: →AB=[−16,8] to →AD=(5}{8}AB ⇒ →AD=[−10,5] ⇒ [x_D−8, y_D+2]=[−10,5] to D(−2,3) a_AB=−0,5 to prosta CD ⊥AB ma równanie CD: y= 2(x−x_D)+y_D ⇒ .... CD: y=2x+7 to C(x,2x+7) Z warunku prostopadłości wektorów AC ⊥BC AC=[x−8,2x+9] i BC=[x+8,2x+1] mamy: (x−8)(x+8)+(2x+9)(2x+1)=0 dokończ ...... otrzymasz dwa takie punkty C spełniające warunki zadania

Eta: Wyżej podałam zad2

Eta:

	5
Poprawiam zapis w pierwszej linijce → AD=		AB→
	8

Eta: Jeszcze zapomniałam ≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈ podkreślnika

nvm: Super, dziękuję pięknie. Zadanie 3 też już rozwiązałem. Eta, jeżeli możesz to utwierdź mnie w przekonaniu. Mianowicie chodzi o to, że przez chwile utknąłem przy zadaniu drugim licząc współrzędne punktu D. Próbowałem liczyć to z długości odcinka i potem porównywałem i problem pojawił się, gdy jedna odpowiedz (−2,3) się pokrywała, a druga wychodziła inna (licząc raz długość AD, a raz BD). Czy w tym przypadku liczyłem punkt, który rzeczywiście znajdował się określoną odległość od wierzchołka i rzeczywiscie znajdował się na prostej, ale już nie na ramieniu, w sensie "moje" D było po przeciwnych stronach. Troche zagmatwanie to napisałem, ale mam nadzieje ze to rozszyfrujecie

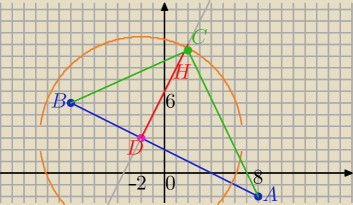
Mila: A(8,−2) B(−8,6) |AD|: |DB|=5:3 1) |AB|²=8²+16²=320 |AB|=8√5 x− wspólna miara 5x+3x=8√5 x=√5 |AD|=5√5, |DB|=3√5 ================ 2) h²=5√5*3√5⇔h²=15*5=75 h=5√3 2) Współrzędne punktu D AB^→[−16,8]

	5
AD→=		*[−16,8]=[−10,5]
	8

A=(8,−2)→T_[−10,5]→D(8−10,−2+5)=(−2,3) 3) DC⊥AB i |DC|=5√3⇔

	1
a) prosta AB: y=−		x+2
	2

Prosta CD: y=2x+b i D∊prostej⇔y=2x+7 √(x+2)²+(y−3)²=(5√3)² (x+2)²+(2x+4)²=75 x=−2−√15 lub x=−2+√15 C₁=(−2+√15,3+2√15) lub C₂=(−2−√15,3−2√15) =====================