 dla ułatwienia (co nie spowoduje błędnego wyniku) ustalmy, że te piłeczki są ponumerowane,
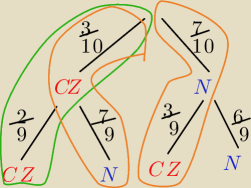
tworzymy drzewko i zaznaczamy 'gałęzie' które spełniają warunki danego podpunktu
i tak :
dla ułatwienia (co nie spowoduje błędnego wyniku) ustalmy, że te piłeczki są ponumerowane,
tworzymy drzewko i zaznaczamy 'gałęzie' które spełniają warunki danego podpunktu
i tak :
| 3 | 2 | |||
Zielone = P(A) = | * | = ... | ||
| 10 | 9 |
| 3 | 7 | 7 | 3 | |||||
Beżowe = P(B) = | * | + | * | = ... | ||||
| 10 | 9 | 10 | 9 |
 )
Więc w pierwszym ciągnięciu musimy wybrać jedną z 3 kul (czerwonych), a w pojemniku jest 10
)
Więc w pierwszym ciągnięciu musimy wybrać jedną z 3 kul (czerwonych), a w pojemniku jest 10
| 3 | ||
kul, więc szansa że to zrobimy wynosi: | ||
| 10 |
| 2 | ||
jest 9 kul ... więc | ||
| 9 |
 )
Więc w pierwszym ciągnięciu musimy wybrać jedną z 3 kul (czerwonych), a w pojemniku jest 10
)
Więc w pierwszym ciągnięciu musimy wybrać jedną z 3 kul (czerwonych), a w pojemniku jest 10
| 3 | ||
kul, więc szansa że to zrobimy wynosi: | ||
| 10 |
| 7 | ||
kul ... więc | ||
| 9 |
