Geometria elementarna Okrąg wpisany pudzian: Hej hej, mam mały problem mam takie zadanie do rozwiązania tylko używając twierdzeń z geometrii elementarnej. Nie mogę użyć ani geometrii analitycznej ani trygonometrii. W trójkąt ABC wpisano okrąg styczny do boków AB, BC, CA odpowiednio w punktach M, N, K. Prosta l przechodząca przez środek D boku AC równolegle do MN przecina proste BC i BA odpowiednio w punktach T i S. Dowieść, że TC = KD = AS.

pudzian:

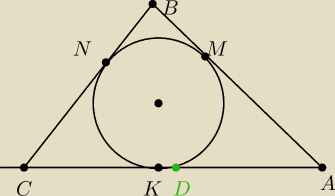
wredulus_pospolitus: narysuj ten trójkąt i pokaż mi jak niby ta prosta ma przechodzić przez punkt D oraz przecinać zarówno BC jak i AB (już pomijam kwestię równoległości do NM)

pudzian: Powinno być przedłużenie zapomniałem dopisać

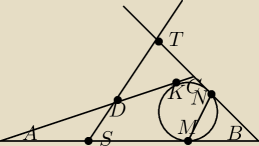
pudzian: O tak to mniej więcej wygląda (udowodnić TC i AS jest łatwo tylko KD pozostaje)

jc: AK=AM CN=CK KC=(1/2)AC−KD KA=(1/2)AC+KD 2KD=KA−KC =AM−CN=(AS+SM)−(TN−CT)=AS+TC Skoro wiesz, że TC=AS, to musi zachodzić równość TC=AS=KD.

pudzian: dzięki ogromne