rozwiąż równanie Enje: podaj liczbę rozwiązań równania 4/(|x+2|−2)=mx w zależności od wartości parametru m

Studentka1roku: D: {|x+2|−2 ≠0 zatem D=R−(−4,0)

4
	−mx=0
|x+2|−2

	4   |x+2|−2
x(		−m)=0
	x

4
	=m
x|x+2|−2x

Teraz z wykresu odczytujemy, że (−∞, 0) 1 rozw., (0,1) 1 rozw., (1,+∞) 3 rozw.

Enje: dziękuję :3 ja próbowałem jakoś tak,,, (po ustaleniu dziedziny) D=R−(−4,0) 4=mx(|x+2|−2) 1) x=(−∞;−4)u(−4;−2) 2) x=<−2;0)u(0;∞) 4=mx(−x−2−2) 4=mx(x+2−2) 0=mx²+4mx+4 0=mx²−4 no i potem deltami tylko że nijak nie chciało wyjść to co w odpowiedziach twój sposób jest super tylko nie do końca wiem jak to narysować przez ten kwadrat w mianowniku, który pojawi się po opuszczeniu wartości bezwzględnej:

4
	=m
x|x+2|−2x

mimo wszystko dziękuję bardzo za pomoc !

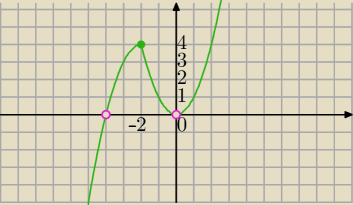Mila: Bez delty: x∊R\{−4,0) mx*(|x+2|−2)=4 dla m= 0 brak rozwiązań

	4
⇔x*(|x+2|−2)=
	m

	4
1) f(x)=x*(|x+2|−2) i y=
	m

x≥−2 i x≠0 f(x)=x² rysujemy wykres paraboli 2) x<−2 wtedy f(x)=−x²−4x x_w=−2, y_w=4 ( pokrywa się z wartością z (1) ) parabola skierowana w dół. 3) Ustalamy liczbę przecięć wykresu

	4
a) jedno rozwiązanie dla		<0⇔m<0
	m

	4
b) 3 rozwiązania dla 0<		<4⇔m>1
	m

	4
c) 2 rozwiązania dla		=4⇔m=1
	m

	4
d) jedno rozwiązanie dla		>4⇔m∊(0,1)
	m

Czy to pokrywa się z odpowiedzią?

Enje: Wszystko bardzo pięknie się pokrywa ja głupi nie wpadłem na to żeby to rozbić [f(x)=... i y=4/m] przez to cały czas miałem ten x² w mianowniku... co zmusiło by mnie do rysowania "na oko" teraz rozumiem dziękuję i życzę miłego wieczoru!

Mila: