 Najmniejszą liczbą całkowitą spełniającą nierównośź x5−4x3−8x2+32>0 jest?
Próbowałam tak:
x3(x2−4)−8(x2−4)>0
(x3−8)(x2−4)>0
x3−8>0
x>2
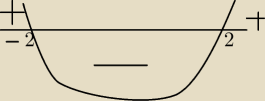
x2−4>0 ( wykres)
x>−2
x>2
Nie wiem jak do tego wykresu "dołożyć" rozwiązanie x3−8>0, zwłaszcza, że w odpowiedziach tą
liczbą jest −1, nie mam pojęcia dlaczego.
Najmniejszą liczbą całkowitą spełniającą nierównośź x5−4x3−8x2+32>0 jest?
Próbowałam tak:
x3(x2−4)−8(x2−4)>0
(x3−8)(x2−4)>0
x3−8>0
x>2
x2−4>0 ( wykres)
x>−2
x>2
Nie wiem jak do tego wykresu "dołożyć" rozwiązanie x3−8>0, zwłaszcza, że w odpowiedziach tą
liczbą jest −1, nie mam pojęcia dlaczego.

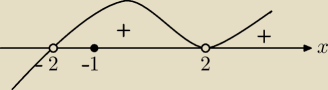 (x3 − 8)(x2 − 4) > 0 ⇒ (x − 2)2(x2 + 2x + 4)(x+2) > 0
(x3 − 8)(x2 − 4) > 0 ⇒ (x − 2)2(x2 + 2x + 4)(x+2) > 0
