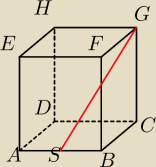
pls salimali: kwadrat ABCD jest podstawą prostopadłościanu ABCDEFGH. odcinek łączacy srodek S krawedzi AB z wierzchołkiem G ma długosc d, a prosta SG jest nachylona do płaszczyzny DCGH pod kątem α. Wyznacz pole powierzchni bocznej prostopadłościanu

wredulus_pospolitus: 'pls' −−− postanowiłeś z okazji nowego roku wrzucić tutaj tuzin zadań i czekać na gotowce

salimali: tuzin zadań których nie rozumiem, uzbierało sie kilka z tego co robiłam dzień w dzień i noc w noc przez całe święta i nowy rok...

wredulus_pospolitus: A na jakim poziomie nauczania jesteś? Czyli mam rozumieć, że nie chcesz gotowca a jedynie 'naprowadzenia'

salimali: tak, chce po prostu zrozumiec, jak bedzie gotowiec to zrozumiem a jak sama podpowiedz to tez moze dam rade a jestem w klasie maturalnej

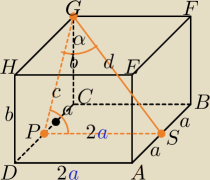
Bogdan: Długość krawędzi podstawy dla wygody obliczeń oznaczam 2a. W trójkącie prostokątnym GPS mając dane miarę kąta α i długość d wyznaczamy 2a oraz c, w trójkącie prostokątnym PCG mając a oraz c wyznaczymy wysokość prostopadłościanu b.

salimali: ten kąt

Mila:

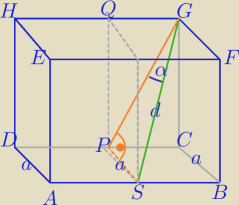
Mila: Licz salimali, jeśli masz odpowiedzi do tych zadań , to też pisz. To już proste zadanie, gdy masz kąt narysowany, w dodatku masz dwa rysunki.

salimali: nie wychodzi mi... a w odp jest 2d²sinα√4−5sin²α

Mila: 1) P_b=4*a*H 2) WΔSPG:

	a
sinα=		⇔a=d*sinα
	d

	|PG|
cosα=		⇔|PG|=d*cosα
	d

3) W ΔPCG:

	a
H2+(		)2=|PG|2
	2

	dsinα)2
H2=(dcosα)2−(
	4

	1
H2=d2cos2α−		*d2 sin2α
	4

	d2
H2=		*(4cos2α−sin2α)
	4

	d2
H2=		*[4*(1−sin2α)−sin2α]
	4

	d2
H2=		*(4−5sin2α)
	4

	d*√4−5sin2α
H=
	2

================ 4)

	d*√4−5sin2α
Pb=4*d*sinα*
	2

P_b=2d²sinα*√4−5sin²α ===================