udowodnij
salimali:
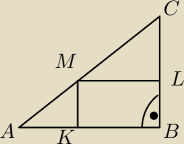
| | IBLI | | IBKI | |
Udowodnij, że |
| + |
| = 1 |
| | IBCI | | IBAI | |
31 gru 11:13
Krzysiek60:
31 gru 11:53
Baba Jaga:
|BL|=|KM| i |BK|=|ML|
Z podobieństwa trójkątów AKM i ABC oraz LMC i ABC
| |BL| | | |AM| | | |BK| | | |MC| | |
| = |
| oraz |
| = |
| |
| |BC| | | |AC| | | |AB| | | |AC| | |
to
| | |BL| | | |BK| | | |AM| | | |MC| | | |AM|+|MC| | | |AC| | |
|
| + |
| = |
| + |
| = |
| = |
| =1 |
| | |BC| | | |AB| | | |AC| | | |AC| | | |AC| | | |AC| | |
31 gru 18:52
Krzysiek60: Dziękuję Baba Jago
31 gru 20:13
Baba Jaga: 
31 gru 20:16
jc: Wygląda to jak równanie odcinkowe prostej: x/a + y/b =1.
Bez podobieństwa trójkątów. Ale za to trzeba wiedzieć, że równanie Ax+By+C=0
określa prostą, o ile (A,B)≠(0,0).
31 gru 20:27

