trójkąt prostokątny
maturka:
Długości wysokości i dwusiecznej poprowadzonych z wierzchołka kąta prostego
w trójkącie prostokątnym są odpowiednio równe m i n
Wyznacz długość okręgu opisanego na tym trójkącie.
30 gru 21:03
Mila:
Eta, liczyłaś może? Ja mam wzór:
30 gru 21:57
Eta:
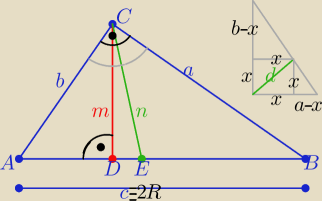
Obwód okręgu opisanego na tym trójkącie
L=2πR = c*π
Należy wyznaczyć długość c −− przeciwprostokątnej w zależności od
m i
n
| | ab | | m*c | |
1/ Z równości pól P= |
| = |
| ⇒ ab=mc |
| | 2 | | 2 | |
2/ długość dwusiecznej
d z podobieństwa Δ ( na szarym rysunku)
| | a | | x | | ab | | ab√2 | |
|
| = |
| ⇒ x= |
| to d=x√2= |
| |
| | b | | b−x | | a+b | | a+b | |
w tym trójkącie d=
n
| | ab√2 | | mc√2 | |
n= |
| ⇒ n= |
| /2 |
| | a+b | | a+b | |
(**) n
2(a+b)
2=2m
2c
2
i z tw. Pitagorasa a
2+b
2=c
2 ⇒ (a+b)
2−2ab=c
2 ⇒ (a+b)
2=c
2+2mc
to z (**) n
2(c
2+2mc)=2m
2c
2 /:c>0
n
2c+2n
2m=2m
2c
| | 2n2m | |
c(2m2−n2)=2n2m ⇒ c= |
| |
| | 2m2−n2 | |
≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈
30 gru 21:59
Eta:
Hej
Mila 
.... i mamy taki sam wynik
Ładne zadanko
30 gru 22:02
Mila:
Tak samo liczyłam, łącznie z wyprowadzeniem wzoru na dł. odcinka dwusiecznej
Nie piszę, tylko od razu wstawiałam c=2R.
30 gru 22:14