Ekstrema lokalne funkcji natali56: Proszę o pomoc w wyznaczeniu ekstremum funkcji f(x) = e * (x²−4x−2)/x² f(x) = (x)³ * (e)⁽2−4x²) Mam nadzieję, że teraz napisałam poprawnie.

iteRacj@: Czy ta druga funkcja to f(x) = x³ * e^(2−4x2)

natali56: Tak

iteRacj@: 1/ ustalenie dziedziny funkcji D=R 2/ obliczenie pierwszej pochodnej f'(x) = (x³)'*e^(2−4x2)+(x³)*(e^(2−4x2))'=−e^(2−4x2)*x²*(8x²−3) i ustalenie dziedziny funkcji pochodnej D'=R 3/ znalezienie miejsc zerowych pochodnej f'(x) = −e^(2−4x2)*x²*(8x²−3) pierwszy czynnik zawsze ujemny więc x²=0 lub 8x²−3=0

	√6		√6
x=		lub x=0 (pierwiastek podwójny) lub x=−
	4		4

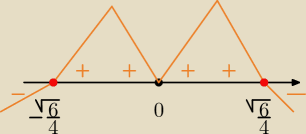
4/ ustalenie dla którego z miejsc zerowych funkcja pochodna zmienia znak

	√6
x=		− → + minimum funkcji
	4

	√6
x=−		+ → − maximum
	4

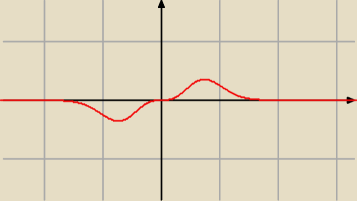
iteRacj@: A tak wygląda wykres tej funkcji. Jeśli coś jest niejasne, to wyjaśnię już jutro.

iteRacj@: przestawiłam minus przepisując, poprawiam 4/ ustalenie dla którego z miejsc zerowych funkcja pochodna zmienia znak

	√6
x=−		− → + minimum funkcji
	4

	√6
x=		+ → − maximum
	4

natali56: Dziękuję bardzo. A może ktoś pomoże w pierwszym przykładzie?

Jerzy: Chętnie. Zacznij od policzenia pochodnej ( dziwna nieco ta stała e w liczniku, no ale skoro tak jest, to wyłacz ją przed pochodną ), potem zastosuj wzór na pochodną ilorazu.

Janek191:

	ex2 − 4 x − 2
f ( x) =		?
	x2

natali56: To jest taka funkcja: f(x) = e⁽(x2−4x−2)/x2) Przepraszam, wcześniej źle odczytałam. e do potęgi ((x2−4x−2)/x2)