Ile liczb całkowitych? nauqa: Ile jest liczb całkowitych spełniających nierówność x²−|x|−2≤0? Zrobiłam to, lecz nie wiem czy poprawnie, więc prosiłabym bardzo o zweryfikowanie tego x≥x²−2 v x≤−x²+2 1. x²−2−x≤0 Δ=9 √Δ=3 x1=−1 x2=2 x∊<−1;2> 2. −x²−x+2≥0 Δ=9 √Δ=3 x1=1 x2=−2 x∊<−2;1> 3. z jedynki i dwójki wynika, że x∊<−2;2>, co oznacza, że nierówność spełnia 5 liczb całkowitych.

Adamm: x²−|x|−2≤0 (|x|+1)(|x|−2)≤0 |x|≤2 −2≤x≤2

PW: Dlaczego nie skorzystasz z parzystości funkcji f(x) = x² − |x| − 2. Oznacza ona, że funkcja przyjmuje takie same wartości dla n jak dla (−n). Wystarczy więc znaleźć rozwiązania będące liczbami całkowitymi dodatnimim czyli rozwiazać nierówność x² − x − 2 ≤ 0 w zbiorze liczb naturalnych (z zerem) i w odpowiedzi podać te liczby oraz liczby do nich przeciwne. (x+1)(x−2) ≤ 0 Rozwiązaniami tej nierówności w zbiorze liczb naturalnych są 0, 1, 2 (tu można dodac rysunek, fragment paraboli tylko dla x≥0), a więc Odpowiedź. Rozwiązaniami nierówności x² − |x| − 2 ≤ 0 są: −2, −1, 0, 1, 2. Wydaje się, że w taki sposób omijamy "rozpatrywanie przypadków" i rozwiązanie jest krótsze.

PW: O, nie widziałem, a Adamm zrobił to lepiej

nauqa: W sumie nie skojarzyłam nawet, że tak jest, gdyż miałam to dość dawno, więc dziękuję bardzo za odpowiedź

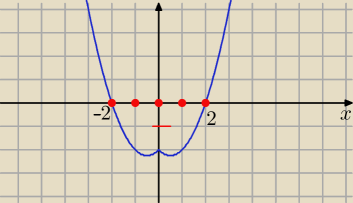
Eta: 5 liczb całkowitych z przedziału <−2,2>