Pole trójkąta- g. analityczna maturzysta: Oblicz pole trójkąta, mając dane dwie proste 4x + 5y + 17 = 0 i x − 3y = 0 zawierające środkowe trójkąta oraz jego wierzchołek A = (−1, −6).

PW: Pewnie trzeba wykorzystać twierdzenie, że środkowe trójkąta przecinają się w jednym punkcie, który dzieli te środkowe w stosunku 2:1 licząc od wierzchołków.

iteRacj@: A nie znasz PW jeszcze jakiegoś twierdzenia dotyczącego środkowych? Po wykorzystaniu tego, o którym piszesz, ma się już współrzędne środka boku BC (−4;1,5), ale zostaje dużo liczenia (dla bardzo pracowitych).

Eta: 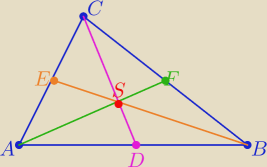Trzy środkowe dzielą trójkąt na sześć trójkątów o równych polach to P(ABC)= 3*P(ABS) ============== 1/ Rozwiązując układ równań prostych zawierających środkowe otrzymasz S(−2,−1)

	−4		17
2/ D∊ : x−3y=0 to D(xD,yD/3) oraz B∊ : 4x+5y+17=0 to B(xB,		xB−		)
	5		5

3/ D jest środkiem odcinka AB zatem 2x_D=x_A+x_B i 2y_D=y_A+y_B po podstawieniu otrzymasz x_B−2x_D=1 i −12x_B−10x_D=145 po rozwiązaniu tego układu otrzymasz B(−8,3) i teraz już z górki

	1
P(ABC)= 3*P(ABS) = 3*		|det(AS,AB)|
	2

....... P(ABC)= 25,5 j² ≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈≈

PW: S=(−3, −1), ale wiedziałem, że to Ty podasz rozwiązanie

Eta: No tak chochlik (S(−3,−1) Dzięki za poprawkę

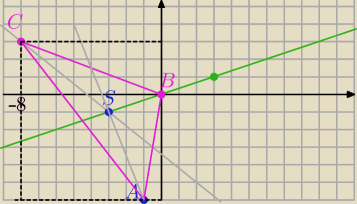
Mila: 1) Punkt przecięcia środkowych: x − 3y = 0 4x + 5y + 17 = 0 S=(−3,−1) punkt przecięcia środkowych (środek ciężkości Δ) 2)Współrzędne środka ciężkości trójkąta o wierzchołkach:

	1		4		17
A(−1,−6), B=(b,		),C(c,−		c−		)
	3		5		5

	−1+b+c
−3=
	3

	−6+13b−45c−175
−1=
	3

stąd b=0, c=−8 B=(0,0), C=(−8,3) 3) P_ΔBSC: BS^→=[−3,−1], BC^→=[−8,3] −3 −1 −8 3 det(..)=17

	17
PΔBSC=
	2

	17		51
4) PΔABC=3*		=
	2		2

=====================