matura probna 7dayz: prosze o pomoc w rozwiazaniu 2 zadan: 1.Zbiorem wszystkich liczb spelniajacych nierownosc |x+3|−|2−x|>=1 jest; A.(−n;−3> B.<0;+n) C.<2;+n) D.<0;2) ;n−nieskonczonosc (sorry nie wiem jak ja zapisac) 2.wiadomo ze log₄9(2)=a oraz log₄9(6)=b. Zatem log₇(48) to: A.6a+2b B.4ab C.12ab D.3a+b 1 robilem metoda autostrady ale mi nie wychodzi

iteRacj@: log₄₉(2)=a log₄₉(6)=b

1
	log7(2)=a
2

1
	log7(6)=b
2

log₇(48)=log₇(6*8)=log₇(6)+log₇(2³) dokończysz?

iteRacj@: To zadanie można rozwiązać na kilka sposobów. Jaka to jest metoda autostrady?

7dayz: wydzielanie miejsc zerowych na osi liczbowej i ustalanie znakow w poszczegolnych wydzielonych przedzialach

iteRacj@: Skorzystałam ze wzoru, którego nie ma w tablicach maturalnych, ale jest łatwy do wyprowadzenia, zapamiętania i często się przydaje. a>0, a≠1, b>0

	1
log(ak)(b)=		loga(b)
	k

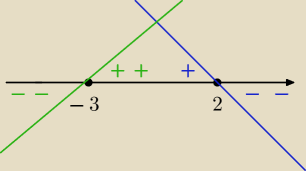
iteRacj@: teraz według tego rysunku ustal przedziały i znaki znak nieskończoności jest pod napisem powrót do spisu zadań

7dayz: https://www.youtube.com/watch?v=tY8RRBeQOXE tu masz przyklad z metoda autostrady dziekuje bardzo. Takie proste a zapomnialo sie jednak

iteRacj@: Ten sposób zaznaczania, który podałam ma tę przewagę nad tym z filmu, że od razu odróżnia się te wyrażenia z wartością bezwzgledną, gdzie występuje −x. Tutaj są często błędy, bo ludzie źle określają znak wyrażenia.

7dayz: ja robilem wlasnie twoim tylko cos mi nie wyszlo

7dayz: nie wiem co ja zle robie I przeddzial po wyznaczeniu iloczynu to x∊(−∞,−3) II x∊<−3,2> III x∊<2,+∞)

iteRacj@: |x+3|−|2−x|≥1 I. (−∞,−3) −(x+3)−(2−x)≥1 −x−3−2+x≥1 −5≥1 sprzeczność → w tym przedziale brak rozwiązań II. <−3,2> (x+3)−(2−x)≥1 2x+1≥1 x≥0 → do zbioru rozwiązań nierówności będą należeć liczby z przedziału <0,2> III. (2,+∞) (x+3)−(−(2−x))≥1 x+3+2−x≥1 5≥1 → do zbioru rozwiązań nierówności będą należeć liczby z przedziału (2,+∞)

iteRacj@: https://www.wolframalpha.com/input/?i=f(x)+%3D+abs(x+%2B+3)-abs(2+-+x)+,+g(x)%3D1

7dayz: Dziękuję ci bardzo