| 1 | ||
Wiedząc, że a + b = 1 uzasadnij, że a4 + b4 ≥ | ||
| 8 |
| 1 | 1 | 1 | 1 | 1 | |||||
a4+ | b4 ≥ ( | a+ | b)4 = | , bo y = x4 jest funkcją wypukłą | |||||
| 2 | 2 | 2 | 2 | 16 |
| 1 | ||
Funkcja f(a)=a(a−1) ma minimum równe | , a więc | |
| 4 |
| 1 | 1 | |||
(2) a4+b4≥2•( | )2= | . | ||
| 4 | 8 |
| 1 | ||
a(a−1)≥ | ||
| 4 |
| 1 | ||
a2−a− | ≥0, | |
| 4 |
| 1 | ||
(a− | )2≥0. | |
| 2 |
| 1 | ||
Oj, uzasadnienie że a(a−1)≥ | złe, ostatnie 5 wierszy nieaktualne. Chyba jednak trzeba | |
| 4 |
| 1 | ||
a(a−1)≥− | , | |
| 4 |
 Spróbuję poprawić. Jest oczywiste, że co najmniej jedna z liczb a, b musi być dodatnia,
przyjmijmy a>0.
Gdyby a>1, to a4>1>1/8 i nie ma czego dowodzić.
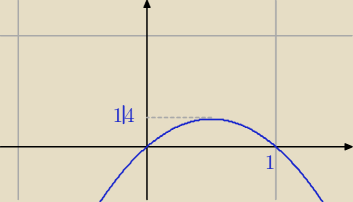
Jeżeli a∊(0,1), to a(1−a)∊(0, 1/4), a więc (a(1−a))2∊(1, 1/16) − nierówność (2) z 22:41 jest
prawdziwa (z tym że uzasadnienie powinno brzmieć:
funkcja f(a)=a(1−a) ma maksimum równe 1/4 ).
Spróbuję poprawić. Jest oczywiste, że co najmniej jedna z liczb a, b musi być dodatnia,
przyjmijmy a>0.
Gdyby a>1, to a4>1>1/8 i nie ma czego dowodzić.
Jeżeli a∊(0,1), to a(1−a)∊(0, 1/4), a więc (a(1−a))2∊(1, 1/16) − nierówność (2) z 22:41 jest
prawdziwa (z tym że uzasadnienie powinno brzmieć:
funkcja f(a)=a(1−a) ma maksimum równe 1/4 ).
| a4+b4 | a+b | |||
4√ | ≥ | /4 | ||
| 2 | 2 |
| 1 | 1 | |||
a4+b4≥ 2* | = | |||
| 16 | 8 |

