Trójkąt Filip: Punkty A=(−7,−2) i B=(4,−7) są wierzchołkami podstawy trójkąta równoramiennego ABC a wysokość opuszczona z wierzchołka A tego trójkąta zawiera się w prostej o równanie 2x+19y+52=0 Oblicz współrzędne wierzchołka C

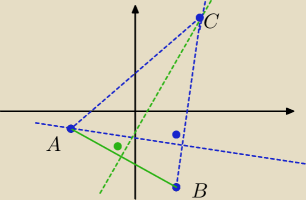
iteRacj@: |AB|=|AC| 1/ wyznacz równanie prostej prostopadłej do 2x+19y+52=0 przechodzącej przez pkt B, w niej będzie się zawierać bok BC a więc na niej leży trzeci wierzchołek − pkt C 2/ wyznacz równanie symetralnej boku AB, na niej również leży trzeci wierzchołek − pkt C 3/ znajdź punkt przecięcia obu prostych czyli wierzchołek C

Janek191:

	2		52
y = −		x −
	19		19

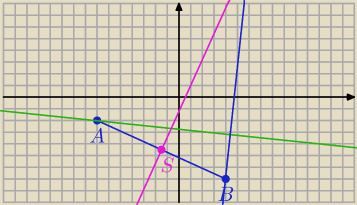
Prosta prostopadła

	19
y =		x + b
	2

	19
− 7 =		*4 + b
	2

− 7 − 38 = b b = − 45

	19
y =		x − 45
	2

S = ( −1,5; −4,5) Prosta AB

	− 7 + 2		5
a =		= −
	4 + 7		11

Prosta prostopadła do pr AB

	11
y =		x + k
	5

	11
− 4,5 =		*(−1,5) + k
	5

− 4,5 + 3,3 = k k = −1,2 y = 2,2 x − 1,2 Rozwiąż układ równań: y = 2,2 x − 1,2 y = 9,5 x − 45 ============ C = ( 6, 12)

Janek191: iteRacj@ AC = BC

iteRacj@: oczywiście, na szczęście na rysunku poprawnie

jc: Wzory odpowiednich prostych można znaleźć prościej (w bardziej zrozumiały sposób?). Prosta prostopadła do prostej 2x+19y+52=0 przechodząca przez B=(4,−7): 19x−2y=19*4+2*7=90. Symetralna odcinka AB, A=(−7,−2) przechodzi przez środek odcinka

	1		1
S=		(A+B)=		(−3,−9) i jest prostopadła do wektora B−A=(11,−5).
	2		2

11x−5y=(−3*11+5*9)/2=6 Przecięcie, czyli punkt C: 19x−2y=90 11x−5y=6 x=6, y=12