Rachunek różniczkowy Olek: Przedstaw liczbę 10 jako sumę dwóch składników tak, aby suma ich sześcianów była najmniejsza ja myślałem tak x+y=10 y=10−x x³+y³=... z tego policzyłem pochodną f'(x)=60x²−300 i minimum wyszło mi dla x=√5 Ale niestety wtedy jest to suma trzech składników, odpowiedzieć to x=5, y=5

Eta: x+y=10 ⇒ y=10−x f(x)=x³+(10−x)³ f(x)= 30x²−300x+1000 −−− f. kwadratowa parabola ramionami do góry osiąga minimum dla odciętej wierzchołka

	−b		300
zatem xmin=		=		=5 to ymin=10−5=5
	2a		60

Olek: Dziękuję, nie zauważyłem błędu w pochodnej. Mam jeszcze pytanie odnoście jednego zadania. Zbadaj liczbę ekstremów funkcji f(x)=ax³+x²+x+b w odp jest, że 1 ekstremum dla a=0, a dlaczego nie jest uwzględnione a=¹₃ przecież f'(x)=3ax²+2x+1 i Δ=4−12a

zys: a czy spełniony jest warunek konieczny ...

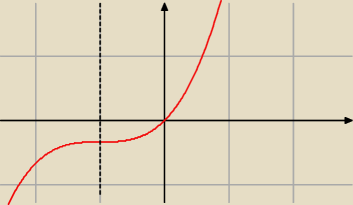
Pytający: Dla a=1/3: f'(x)=0 dla x=−1 f'(x)>0 dla x≠−1

	x3
Powyżej wykres f(x)=		+x2+x, znaczy dla b=0 (zmiana b spowoduje jedynie przesunięcie
	3

wykresu góra−dół, ale kształt będzie taki sam).

Olek: Ok już chyba rozumiem, gdy a={1}{3} to pochodna nie zmienia znaku i wtedy nie istnieje ekstremum