Postać trygonometryczna liczby zespolonej natali56: Ponownie muszę prosić o pomoc. Mam w domu studenta I roku politechniki, który ma problemy z matematyką. Sama studiowałam ponad 20 lat temu i już nie potrafię sobie poradzić z trudniejszymi zadaniami. Niestety. Przedstaw w postaci trygonometrycznej liczbę: −4/1+√3i −4/√3 −i

piotr: a + i b = √a²+b² e^arctg(b/a)i = √a²+b² ( cos(arctg(b/a)) + i sin(arctg(b/a)) )

grzest: No tak, rozumiem. Ale o nawiasach pamiętać należy, choćby minęło wiele lat. Zadanie 1. Wg mnie liczba ta ma następującą postać:

	−4		−4(1−√3i)		1−√3i
z =		=		= −4		= −1+√3i.
	1+√3i		(1+√3i)(1−√3i)		4

Moduł z oznaczę jako r r=√x¹+y² = √(−1)²+(√3)² = 2.

	x		1
cos φ =		= −		⇒ φ = 2π/3.
	r		2

Postać trygonometryczna:

	2π		2π
z= r(cos φ + i sin φ) = 2(cos		+i sin		).
	3		3

Zad. 2 liczymy podobnie.

natali56: Zgadzam się. Dokładnie ma taką postać. Nie umiałam jej tak zapisać. Jednak nie rozumiem o jakich nawiasach zapomniałam. Za moich czasów pisało się ręcznie. Bardzo dziękuję za pomoc. Mam nadzieję, że z drugim sobie poradzę. Pewnie jeszcze nie raz będę potrzebowała pomocy.

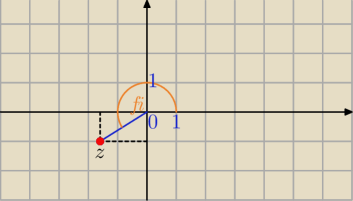
Mila: z=−4/(√3 −i)

	−4		√3+i		−4*(√3+i)
z=		*		=
	√3−i		√3+i		3−i2

	−4*(√3+i)
z=
	4

z=−√3−i |z|=√(√3)²+1¹=2

	√3
cosφ=−
	2

	1
sinφ=−
	2

φ− kąt z III ćwiartki ( punkt (−√3,−1) leży w III ćwiartce)

	π
φ=π+
	6

	7π		7π
z=2*(cos		+i sin		)
	6		6

==================

PW: A nawiasy są niezbędne, gdy używamy "/" zamiast kreski ulamkowej. Przecież −4/1+√3i to nie to samo co −4/(1+√3i).

Jerzy: A ja bym wynajął studentce polonistyki i miał problem z głowy.

natali56: Ok. Rozumiem.

daras: a najlepiej jakby sam poszedł na polonistykę bez znajomości matematyki sprzed roku na PW sobie nie poradzi