Rozwiąż nierówność trygonometryczną. Matt: Funkcja f jest określona wzorem f(x) = sinx dla x <0; 2PI>. Rozwiąż nierówność f(2x) >= 2(f(x))². Czyli mam rozwiązać sin2x >= 2(sinx)² dla x <0; 2PI> Jakieś podpowiedzi?

Janek191: f(2 x) = sin 2x 2 (f(x))² = 2 sin² x sin 2 x ≥ 2 (sin x)² sin2 x = 2 sin x*cos x

Adamm: sin(2x) = 2sin(x)cos(x)

Mila: sin2x≥2sin²x⇔ 2sinx*cosx−2sin²x≥0 2sinx*(cosx−sinx)≥0 i x∊<0,2π>

	π
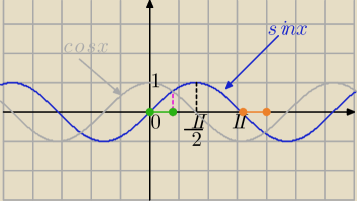
1) sinx≥0 i cosx≥sinx⇔x∊<0,π> i x∊<0,		>⇔ patrz na wykres:
	4

	π
x∊<0,		>
	4

lub 2) sinx≤0 i cosx≤sinx i x∊<0,2π> dokończ

Matt: 2sinxcox>=2(sinx)² sinxcox−(sinx)²>=0 sinx(cosx−sinx)>=0 co dalej :x

Matt: a ok dziękuję

Mila: I co dalej napisałeś, aby dokończyć?

Matt: x∊<π; 5/4π>

Mila: Dobrze

Jan: Dlaczego rozwiązujemy przypadek nr 2, tzn. sin(x)≤0 i cos(x)≤sin(x)