graniastosłupy
matfizo: Podstawą graniastosłupa prostego jest trójkąt równoramienny o ramieniu a i kącie α przy
podstawie tego trójkąta. Graniastosłup ten przecięto płaszczyzną przechodzącą przez
wierzchołek jednej podstawy, leżący między ramionami, i krawędź drugiej podstawy, leżący
naprzeciw tego wierzchołka. Płaszczyzna ta tworzy z płaszczyzną podstawy graniastosłupa kąt β.
Oblicz pole powierzchni bocznej i objętość graniastosłupa.
26 gru 17:22
iteRacj@:
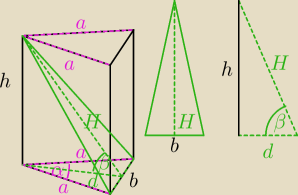 obliczamy pole podstawy:
obliczamy długość trzeciego boku trójkąta w podstawie:
obliczamy pole podstawy:
obliczamy długość trzeciego boku trójkąta w podstawie:
b
2=a
2+a
2−2a*a*cos α, b>0
b
2=2a
2(1−cos α) \\ tw. cosinusów
b=
√2a2(1−cos α)=a
√2(1−cos α)
obliczamy długość wysokości trójkąta w podstawie:
| 1 | | 1 | |
| d*b= |
| a2*sin α \\ wzory na pola podstawy |
| 2 | | 2 | |
obliczamy wysokość graniastosłupa:
obliczamy objętość graniastosłupa:
| | 1 | | a2sin α | | 1 | | a3sin2α*tg β | |
V= |
| * |
| *tg β* |
| *a2sinα= |
| |
| | 3 | | b | | 2 | | 6√2(1−cos α) | |
26 gru 18:46
iteRacj@: W treści zadania kąt α jest przy podstawie trójkąta, a na moim rysunku między ramionami,
więc rozwiązanie do poprawki niestety.
26 gru 18:50
piotr: | | a3 | |
V = |
| sin(π−2α)cos(π/2−α)tgβ |
| | 2 | |
26 gru 19:25
iteRacj@:
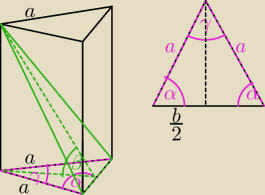 poprawione
poprawione
γ=180
o−2α
obliczamy pole podstawy:
| | 1 | | 1 | | 1 | |
Pp= |
| a*a*sin γ= |
| a*a*sin(180o−2α)= |
| a2sin(2α) |
| | 2 | | 2 | | 2 | |
obliczamy długość trzeciego boku trójkąta w podstawie:
| | b/2 | |
cos α= |
| b/2=a*cos α b=2a*cos α |
| | a | |
obliczamy długość wysokości trójkąta w podstawie:
| 1 | | 1 | |
| d*b= |
| a2*sin γ \\ wzory na pola trójkątów |
| 2 | | 2 | |
| | a2sin γ | | a2sin(180o−2α) | | a2sin(2α) | | a*sin(2α) | |
d= |
| = |
| = |
| = |
| |
| | b | | b | | 2a*cos α | | 2cos α | |
obliczamy wysokość graniastosłupa:
| | a*sin(2α) | |
h=d*tg β= |
| *tg β=a*sin α*tg β |
| | 2cos α | |
obliczamy objętość graniastosłupa:
| | 1 | | 1 | | 1 | |
V= |
| *a*sin α*tg β* |
| a2sin(2α)= |
| *a3*sin α*tg β*sin(2α) |
| | 3 | | 2 | | 6 | |
26 gru 19:31
iteRacj@: oczywiście wzór na objetość graniastosłupa tak jak u
piotra bez 1/3
| | 1 | |
V= |
| a3*sin α*tg β*sin(2α) |
| | 2 | |
26 gru 19:35

 poprawione
poprawione